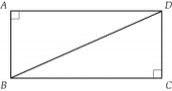
Rectangle
In a rectangle with sides, 8 and 9 mark the diagonal. What is the probability that a randomly selected point within the rectangle is closer to the diagonal than any side of the rectangle?
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Would you like to compute the count of combinations?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Determine 82341
 Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1].
Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1]. - The length 17
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - Quadrilateral 78874
 Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
- Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - ABS, ARG, CONJ, RECIPROCAL
 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - A chord
 In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the cord at the center of the circle Hence find the length of the minor arc cut off by the chord.
In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the cord at the center of the circle Hence find the length of the minor arc cut off by the chord. - A circle 2
 A circle is centered at the point (-7, -1) and passes through the point (8, 7). The radius of the circle is r units. The point (-15, y) lies in this circle. What are r and y (or y1, y2)?
A circle is centered at the point (-7, -1) and passes through the point (8, 7). The radius of the circle is r units. The point (-15, y) lies in this circle. What are r and y (or y1, y2)? - Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
- Radio radius
 Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both
Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both - Draw triangle
 Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37°
Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37° - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Three
 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Regular octagon pad
 You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci
- Angle ASB
 On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets.
On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets. - Circle inscribed
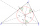 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
