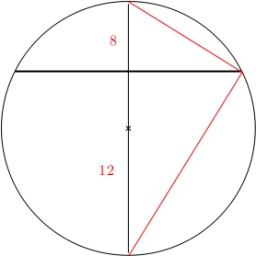
Two chords
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- similarity of triangles
- algebra
- quadratic equation
- equation
- system of equations
- expression of a variable from the formula
- biquadratic equation
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- triangle
- chord
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Right-angled 27683
 Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles.
Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles.
- Conical bottle
 When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle?
When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle? - Sides of right angled triangle
 One leg is 1 m shorter than the hypotenuse, and the second leg is 2 m shorter than the hypotenuse. Find the lengths of all sides of the right-angled triangle.
One leg is 1 m shorter than the hypotenuse, and the second leg is 2 m shorter than the hypotenuse. Find the lengths of all sides of the right-angled triangle. - Secret treasure
 Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure.
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure. - Euclid theorems
 Calculate the sides of a right triangle if leg a = 6 cm and a section of the hypotenuse, which is located adjacent to the second leg b, is 5cm.
Calculate the sides of a right triangle if leg a = 6 cm and a section of the hypotenuse, which is located adjacent to the second leg b, is 5cm. - A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
- A cone 4
 A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts. - Mast angles and height
 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Vertex of the rectangle
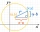 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Quadratic equation - Viets
 In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas.
In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas. - Properties of eq2 roots
 If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq.
If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq.
- Evaluate 37
 Evaluate the function K(x) = 2x²+3x-2 what is the value of K(½)
Evaluate the function K(x) = 2x²+3x-2 what is the value of K(½) - Fredrik
 Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b.
Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b. - Width and length
 For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
