Dve tětivy
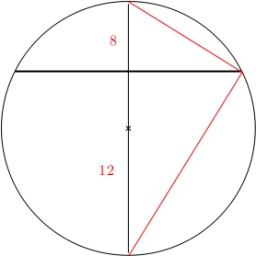
Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm.
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Tětiva
Je dána kružnice k (S, 5cm). Vypočítejte délku tětivy kružnice k, jestliže je od středu S vzdálena 3cm. - Poloměr 10
Poloměr kružnice r=8,9 cm, tětiva AB této kružnice má délku 16 cm. Vypočítej vzdálenost tětivy AB od středu kružnice . - Vypočítej tětivu
Vypočítej délku tětivy kružnice, která je vzdálena od středu kružnice 2,5 cm. Poloměr je 6,5 cm. - Tětiva 2
Bod A má od středu kružnice s poloměrem r = 5 cm vzdálenost 13 cm. Vypočítejte délku tětivy spojující body dotyku T1 a T2 tečen vedených z bodu A ke kružnici k. - Tětiva - vzdálenost
V kružnici k (S; 6cm) vypočítejte vzdálenost tětivy t od středu kružnice S, pokud délka tětivy je t = 10cm. - Tětiva
Vypočítejte délku tětivy, jejíž vzdálenost od středu S kružnice k (S, 22 cm) se rovná 12 cm. - Vypočítejte - tětiva
Tětiva PQ je dlouhá 10,4 cm a její vzdálenost od středu kruhu je 3,7 cm. Vypočítejte délku druhé tětivy RS, která je 4,1 cm od středu této kružnice.
