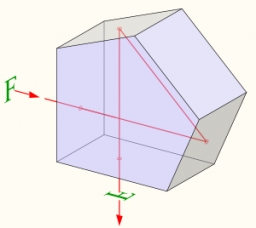
Pentagonal prism
The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- surface area
- prism
- planimetrics
- circle
- polygon
- area of a shape
- goniometry and trigonometry
- sine
- cosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Pump power
 Determine the pump power if: I pour 3 m³ of water from the tank in 120 seconds with a hose. The height of the hose mouth above the tank is 1.5 m. The water's speed from the hose outlet is 20 m/s.
Determine the pump power if: I pour 3 m³ of water from the tank in 120 seconds with a hose. The height of the hose mouth above the tank is 1.5 m. The water's speed from the hose outlet is 20 m/s. - Temperature 7477
 The pool with a length of l = 50 m and a width of s = 15 m has a depth of h1 = 1.2 m at the shallowest part of the wall. The depth then gradually increases to a depth of h2 = 1.5 m in the middle of the pool. = 4.5 m walls in the deepest part of the pool.
The pool with a length of l = 50 m and a width of s = 15 m has a depth of h1 = 1.2 m at the shallowest part of the wall. The depth then gradually increases to a depth of h2 = 1.5 m in the middle of the pool. = 4.5 m walls in the deepest part of the pool. - Orlík hydroelectric plant
 The Orlík hydroelectric power plant, built in 1954-1961, consists of four Kaplan turbines. For each of them, the water with a flow rate of Q = 150 m3/s is supplied with a flow rate of h = 70.5 m at full power. a) What is the total installed pow
The Orlík hydroelectric power plant, built in 1954-1961, consists of four Kaplan turbines. For each of them, the water with a flow rate of Q = 150 m3/s is supplied with a flow rate of h = 70.5 m at full power. a) What is the total installed pow - What power 2
 What power has a pump output to move 4853 hl of water to a height of 31 m for 8 hours? Comparing the power generated by the pump vs. the power generated by the motor, which is more efficient? Which pump or motor generates more pollution if, for every watt
What power has a pump output to move 4853 hl of water to a height of 31 m for 8 hours? Comparing the power generated by the pump vs. the power generated by the motor, which is more efficient? Which pump or motor generates more pollution if, for every watt
- Radiators
 Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1
Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1 - Concrete column
 The concrete column of the highway bridge has the shape of a block with dimensions of 1m x 0.8m x 25m. Crane should lift it to a height of 20m. What is the power of his engine if the lifting takes 2 minutes?
The concrete column of the highway bridge has the shape of a block with dimensions of 1m x 0.8m x 25m. Crane should lift it to a height of 20m. What is the power of his engine if the lifting takes 2 minutes? - Pump
 What power does a pump output to move 4853 hl of water to a height of 31 m for 8 hours?
What power does a pump output to move 4853 hl of water to a height of 31 m for 8 hours? - Cu thief
 The thief stole 142 meters copper wire with a cross-section area of $s mm². Calculate how much money gets in the scrap redemption if redeemed copper for 5.3 Eur/kg. The density of copper is 8.96 t/m³.
The thief stole 142 meters copper wire with a cross-section area of $s mm². Calculate how much money gets in the scrap redemption if redeemed copper for 5.3 Eur/kg. The density of copper is 8.96 t/m³. - Acceleration 79164
 A skier goes down a slope 66 m long in a uniformly accelerated motion in 10 seconds. With what acceleration was it moving, and what is the slope of the slope?
A skier goes down a slope 66 m long in a uniformly accelerated motion in 10 seconds. With what acceleration was it moving, and what is the slope of the slope?
- Approximately 30131
 Please calculate according to Pascal's law. Calculate the hydrostatic pressure at a depth of 300m below sea level if the density of seawater is approximately 1025kg per m³. At what depth below the surface is the hydrostatic pressure 4.5 MPa?
Please calculate according to Pascal's law. Calculate the hydrostatic pressure at a depth of 300m below sea level if the density of seawater is approximately 1025kg per m³. At what depth below the surface is the hydrostatic pressure 4.5 MPa? - Compressive 19933
 The submarine is at a depth of 50 m below the concave surface of the sea. Find the hydrostatic compressive strength of seawater on a metal cover with an area of 0.6 m².
The submarine is at a depth of 50 m below the concave surface of the sea. Find the hydrostatic compressive strength of seawater on a metal cover with an area of 0.6 m². - A car
 A car weighing 1.05 tonnes driving at the maximum allowed speed in the village (50 km/h) hit a solid concrete bulkhead. Calculate height would have to fall on the concrete surface to make the impact intensity the same as in the first case!
A car weighing 1.05 tonnes driving at the maximum allowed speed in the village (50 km/h) hit a solid concrete bulkhead. Calculate height would have to fall on the concrete surface to make the impact intensity the same as in the first case! - Copper sheet
 The copper plate has a length of 2.2 m, width 92 cm, and weighs 5.6 kg. What is the plate thickness if 1 m³ weighs 8732 kg?
The copper plate has a length of 2.2 m, width 92 cm, and weighs 5.6 kg. What is the plate thickness if 1 m³ weighs 8732 kg? - Complete 16
 Complete the conversions below, show calculations and answers 1) 3.5 kg to gram 2) 4567ml to litres 3) R45.78 to cent 4) 5.60m to centimeters
Complete the conversions below, show calculations and answers 1) 3.5 kg to gram 2) 4567ml to litres 3) R45.78 to cent 4) 5.60m to centimeters
- Heat energy
 Energy is measured using the unit Joule (J). Temperature is measured using the unit degree Celsius °C). To increase the temperature of 1 liter of water by 1°C, 4200 J of heat energy is required. (a) Kelly wants to increase the temperature of 2 liters of w
Energy is measured using the unit Joule (J). Temperature is measured using the unit degree Celsius °C). To increase the temperature of 1 liter of water by 1°C, 4200 J of heat energy is required. (a) Kelly wants to increase the temperature of 2 liters of w - Coefficient 81094
 A car moves along a horizontal road at a speed of 15 m/s. After turning off the engine, the car traveled a distance of 225 m. What was the coefficient of friction for this motion?
A car moves along a horizontal road at a speed of 15 m/s. After turning off the engine, the car traveled a distance of 225 m. What was the coefficient of friction for this motion? - Cross-sectional 80979
 An undisciplined motorcyclist drove at an unreasonable speed on a mountain road, lost control in a bend, and left the roadway at 90 km/h. He was falling into a gully 36 m deep. Draw a cross-sectional picture of the whole situation. How far did the motorcy
An undisciplined motorcyclist drove at an unreasonable speed on a mountain road, lost control in a bend, and left the roadway at 90 km/h. He was falling into a gully 36 m deep. Draw a cross-sectional picture of the whole situation. How far did the motorcy
