Pětiboký hranol
Pravidelný pětiboký hranol je vysoký 10 cm. Poloměr kružnice opsané podstavě je 8 cm. Vypočtěte objem a povrch hranolu.
Vaše odpověď:
Vaše odpověď:
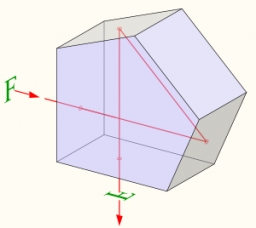
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Nejpřirozenější aplikací trigonometrie a goniometrických funkcí představuje výpočet trojúhelníků. Běžné i méně běžné výpočty různých typů trojúhelníků nabízí naše trigonometrická kalkulačka trojúhelníku. Slovo trigonometrie pochází z řečtiny a doslovně znamená výpočet trojúhelníku.
Nejpřirozenější aplikací trigonometrie a goniometrických funkcí představuje výpočet trojúhelníků. Běžné i méně běžné výpočty různých typů trojúhelníků nabízí naše trigonometrická kalkulačka trojúhelníku. Slovo trigonometrie pochází z řečtiny a doslovně znamená výpočet trojúhelníku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Pravidelný hexagon
Pravidelný šestiboký hranol je vysoký 2 cm. Poloměr kružnice opsané podstavě je 8 cm. Určete jeho objem a povrch. - Hexagon, hexa S,V
Jaký je povrch a objem pravidelného šestibokého hranolu s hranou podstavy 12 cm a výškou hranolu rovnou průměru kružnice opsané podstavě. - Povrch a objem
Vypočítejte povrch a objem válce jehož výška je 8 dm a poloměr kružnice podstavy je 2 dm - Trojboký hranol
Pravidelný trojboký hranol je vysoký 7 cm. Jeho podstava je rovnostranný trojúhelník, jehož výška je 3 cm. Vypočítejte povrch a objem tohoto hranolu. - Šestiúhelníkový hranol
Podstavou hranolu je pravidelný šestiúhelník, který je složen ze šesti trojúhelníků se stranou a = 12 cm a výškou va = 10,4 cm. Výška hranolu je 5 cm. Vypočítejte objem a povrch hranolu! - Vypočtěte 12
Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm - Pravidelný n-uhelnik
Který pravidelný n-uhelnik má poloměr opsane kružnice r=10 cm, a poloměr vepsané kružnice p=9,962 cm?
