Planimetrics - math word problems - page 150 of 185
Number of problems found: 3688
- MO Z6-I-2 2017
 Erika wanted to offer chocolate to her three friends. When she took it out of her backpack, she found that it was broken, as shown in the picture. (The marked squares are identical.) The girls have agreed not to break the chocolate anymore and will draw l
Erika wanted to offer chocolate to her three friends. When she took it out of her backpack, she found that it was broken, as shown in the picture. (The marked squares are identical.) The girls have agreed not to break the chocolate anymore and will draw l - An archer
 An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to
An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to - Two rectangles
 I cut out two rectangles with 54 cm² and 90 cm². Their sides are expressed in whole centimeters. If I put these rectangles together, I get a rectangle with an area of 144 cm². What dimensions can this large rectangle have? Write all options. Explain your
I cut out two rectangles with 54 cm² and 90 cm². Their sides are expressed in whole centimeters. If I put these rectangles together, I get a rectangle with an area of 144 cm². What dimensions can this large rectangle have? Write all options. Explain your - Motorcyclist and a car
 The passenger car left at 7:00 and was heading east at a speed of 60 km/h. A motorcyclist left the same place and headed north at 40 km/h. What will be their air distance at ten o'clock?
The passenger car left at 7:00 and was heading east at a speed of 60 km/h. A motorcyclist left the same place and headed north at 40 km/h. What will be their air distance at ten o'clock? - The tangent of the hyperbola
 Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4].
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4]. - Quadrilateral ABCD
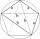 Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125°
Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125° - Triangle SSA
 Construct a triangle ABC if |AB| = 5cm va = 3cm, CAB = 50 °. It is to create the analysis and construction steps.
Construct a triangle ABC if |AB| = 5cm va = 3cm, CAB = 50 °. It is to create the analysis and construction steps. - Engine pulley
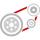 The engine has a 1460 rev/min (RPM). The disc diameter is 350 mm. What will be the peripheral disc speed in RPM? Pulleys on the engine have a diameter of 80mm, and a disc has a diameter of 160mm.
The engine has a 1460 rev/min (RPM). The disc diameter is 350 mm. What will be the peripheral disc speed in RPM? Pulleys on the engine have a diameter of 80mm, and a disc has a diameter of 160mm. - Train
 The train is running at speeds of 98 km/h. From the beginning of braking to full stop, the train runs for 2 minutes. If the train slows the braking equally, calculate the distance from the location where you need to start to brake.
The train is running at speeds of 98 km/h. From the beginning of braking to full stop, the train runs for 2 minutes. If the train slows the braking equally, calculate the distance from the location where you need to start to brake. - Plot Map Scale
 The rectangular plot has dimensions of 50 m and 100 meters. On the plain, its circumference is 60 cm. To what extent is the plan made?
The rectangular plot has dimensions of 50 m and 100 meters. On the plain, its circumference is 60 cm. To what extent is the plan made? - Square diagonal construction
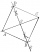 There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you
There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you - Rectangle drawing calculation
 Draw rectangles. Color them and calculate the circuits and areas. KLMN: KL = 5CM LM = 3CM rectangle OPQR OP = 4cm PQ = 3.5cm
Draw rectangles. Color them and calculate the circuits and areas. KLMN: KL = 5CM LM = 3CM rectangle OPQR OP = 4cm PQ = 3.5cm - Trapezoid construction
 Draw an isosceles trapezoid ABDC if a = 6cm, v = 5cm, beta = 60 degrees. / sketch, procedure, construction /
Draw an isosceles trapezoid ABDC if a = 6cm, v = 5cm, beta = 60 degrees. / sketch, procedure, construction / - Trapezoid construction
 Construct an isosceles trapezoid, whose base is 6 cm long, the base forms an angle of 30 ° with the diagonal, and the arms are 4 cm long.
Construct an isosceles trapezoid, whose base is 6 cm long, the base forms an angle of 30 ° with the diagonal, and the arms are 4 cm long. - Triangle from sticks
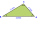 Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks?
Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks? - Parallels and one secant
 There are two different parallel lines, a, b, and line c, that intersect the two parallel lines. Draw a circle that touches all lines at the same time.
There are two different parallel lines, a, b, and line c, that intersect the two parallel lines. Draw a circle that touches all lines at the same time. - Construct
 Construct a triangle ABC inscribed circle with a radius r = 2 cm and an angle alpha = 50 degrees = 8 cm. Make a sketch, analysis, construction, and description.
Construct a triangle ABC inscribed circle with a radius r = 2 cm and an angle alpha = 50 degrees = 8 cm. Make a sketch, analysis, construction, and description. - Outer contact of circles
 Construct a circle k1 (S1; 1.5 cm), k2 (S2; 2 cm), and K3 (S3; 2.5 cm) so that they are always two outer contacts. Calculate the perimeter of the triangle S1S2S3.
Construct a circle k1 (S1; 1.5 cm), k2 (S2; 2 cm), and K3 (S3; 2.5 cm) so that they are always two outer contacts. Calculate the perimeter of the triangle S1S2S3. - Coordinates hexagon
 The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle.
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle. - The tangent line
 Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1.
Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
