Planimetrics - math word problems - page 149 of 185
Number of problems found: 3685
- Pasture 79214
 I need to find out the number of bulls in the third period. In the first period, 12 bulls grazed on 3 and 1/3 ha for 4 weeks. In the second period, 21 bulls graze on 10 ha for 9 weeks. How many bulls in the third period graze for 24ha and 18 weeks? The pa
I need to find out the number of bulls in the third period. In the first period, 12 bulls grazed on 3 and 1/3 ha for 4 weeks. In the second period, 21 bulls graze on 10 ha for 9 weeks. How many bulls in the third period graze for 24ha and 18 weeks? The pa - Draw triangle
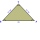 Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm.
Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm. - Telephone calls
 The random variable that models the time between 2 phone calls has an exponential distribution with density f(x)=10exp (-10x), x is greater than 0. Calculate its distribution function and the probability that the time between calls does not exceed 5 secon
The random variable that models the time between 2 phone calls has an exponential distribution with density f(x)=10exp (-10x), x is greater than 0. Calculate its distribution function and the probability that the time between calls does not exceed 5 secon - MO8-Z8-I-5 2017
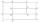 Identical rectangles ABCD and EFGH are positioned such that their sides are parallel to the same. The points I, J, K, L, M, and N are the intersections of the extended sides, as shown. The area of the BNHM rectangle is 12 cm2, the rectangle MBC
Identical rectangles ABCD and EFGH are positioned such that their sides are parallel to the same. The points I, J, K, L, M, and N are the intersections of the extended sides, as shown. The area of the BNHM rectangle is 12 cm2, the rectangle MBC - Meridian ground speed
 The plane flies south at an average speed of 190 km/h, and the wind blows from west to east at a speed of 20 m/s. How fast and in what direction (relative to the meridian) will the plane move relative to the ground?
The plane flies south at an average speed of 190 km/h, and the wind blows from west to east at a speed of 20 m/s. How fast and in what direction (relative to the meridian) will the plane move relative to the ground? - The bomber
 An aircraft flying at an altitude of 1260 m. From what distance in front of the target must a parachute load be dropped from an airplane? The load slopes at a speed of 5.6 m/s and moves in the direction of movement at 12 m/s. What is the direct distance o
An aircraft flying at an altitude of 1260 m. From what distance in front of the target must a parachute load be dropped from an airplane? The load slopes at a speed of 5.6 m/s and moves in the direction of movement at 12 m/s. What is the direct distance o - An archer
 An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to
An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to - MO Z6-I-2 2017
 Erika wanted to offer chocolate to her three friends. When she took it out of her backpack, she found that it was broken, as shown in the picture. (The marked squares are identical.) The girls have agreed not to break the chocolate anymore and will draw l
Erika wanted to offer chocolate to her three friends. When she took it out of her backpack, she found that it was broken, as shown in the picture. (The marked squares are identical.) The girls have agreed not to break the chocolate anymore and will draw l - Quadrilateral ABCD
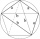 Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125°
Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125° - Diagonals 14073
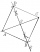 There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you
There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you - Construct 4129
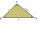 Construct a triangle ABC, given the lengths of the sides: c = 8 cm, a = 5 cm and height length hc = 3.5 cm. Perform an analysis, write down the design procedure, perform it, and determine the number of solutions.
Construct a triangle ABC, given the lengths of the sides: c = 8 cm, a = 5 cm and height length hc = 3.5 cm. Perform an analysis, write down the design procedure, perform it, and determine the number of solutions. - Perpendicular diameters
 Draw a circle k/S; 4.5 cm/. Next, draw: a/two mutually perpendicular diameters AB and CD b/two radii SA and SE which form an angle of 75 degrees c/chord/KL/= 4 cm d/chord/MN/, which is perpendicular to KL
Draw a circle k/S; 4.5 cm/. Next, draw: a/two mutually perpendicular diameters AB and CD b/two radii SA and SE which form an angle of 75 degrees c/chord/KL/= 4 cm d/chord/MN/, which is perpendicular to KL - Forces on earth directions
 A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object?
A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object? - Complete construction
 Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs.
Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs. - Quadrilaterals II
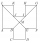 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M and divide the dodecago
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M and divide the dodecago - Square grid
 A square grid consists of a square with sides of a length of 1 cm. Draw at least three patterns, each with an area of 6 cm² and a circumference of 12 cm, and their sides in a square grid.
A square grid consists of a square with sides of a length of 1 cm. Draw at least three patterns, each with an area of 6 cm² and a circumference of 12 cm, and their sides in a square grid. - Constructed 67424
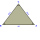 There are six lines 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm long, two of each length. How many isosceles triangles can be constructed from them? List all options.
There are six lines 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm long, two of each length. How many isosceles triangles can be constructed from them? List all options. - Isosceles 6673
 Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long.
Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long. - Individual
 To prepare 14 kg of cheese with 45% dry matter, 3 types of cheese mixtures were mixed. The first was 5 kg, the second was 3 kg and had 14% more dry matter (14 percentage points more) than the first. The third mixture, which had 2 times as much dry matter
To prepare 14 kg of cheese with 45% dry matter, 3 types of cheese mixtures were mixed. The first was 5 kg, the second was 3 kg and had 14% more dry matter (14 percentage points more) than the first. The third mixture, which had 2 times as much dry matter - The tangent line
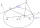 Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1.
Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
