Podobnosť trojuholníkov - príklady - strana 4 z 8
Pokyny: Vyriešte každú úlohu starostlivo a ukážte svoje celé riešenie. Ak je to vhodné, vykonajte skúšku správnosti riešenia.Počet nájdených príkladov: 157
- Výškový uhol
Pozoroval stojaci západne od veže vidí jej vrchol pod výškovým uhlom 45 stupňov. Potom, čo sa posunie o 50 metrov na juh, vidí jej vrchol pod výškovým uhlom 30 stupňov. Ako vysoká je veža? - Budova tieň
Aký dlhý tieň vrhá budova vysoká 15 m, ak tieň metrovej tyče je 90 cm. Načrtni si - podobnosť. - Rozdeliť rezom
Daný je kužeľ s polomerom podstavy 10 cm a výškou 12 cm. V akej výške nad podstavou ho máme rozdeliť rezom rovnobežným s podstavou, aby objemy oboch vzniknutých teles boli rovnaké? Výsledok uveďte v cm. - Pozorovateľ 3
Pozorovateľ vidí vrcholce dvoch stromov v rovnakom uhle α. Od jedného stromu je vzdialený 9 m, od druhého 21 m. Stromy stoja na rovine. Aký vysoký je druhý strom, ak výška prvého je 6 m? Nezabudni, že oči stojaceho človeka sú približne 1,5 m nad zemou. - Tieň stromu
Tieň 1 m vysoké tyče vrhnutý na vodorovnú rovinu má dĺžku 0,8 m. V rovnakom okamihu má tieň stromu vrhnutý na vodorovnú rovinu 6,4 m. Urči výšku stromu. - Dané sú 2
Dané sú trojuholníky KLM a ABC, ktoré sú navzájom podobné. Dopočítaj dĺžky zvyšných strán trojuholníka KLM, ka dĺžky trán sú a=7 b=5,6 c=4,9 k=5 - Rozhľadňa
Vypočítaje výšku rozhľadne vrhajúce tieň 36 m, ak v rovnakom čase stĺp vysoký 2,5 m má tieň 1,5 m. - Trojuholník 49
Trojuholník KLM má dĺžku strán k=6,3cm, l=8,1cm, m=11,1cm. Trojuholník XYZ má dĺžku strán x=8,4cm, y= 10,8cm, z= 14,8cm. Sú trojuholníku KLM a XYZ podobné? (zapíš 0 ak nie, ak áno, nájdi a zapíš koeficient podobnosti) - Nádoba
Uzavretá nádoba v tvare kužeľa stojaca na svojej podstave je naplnená vodou tak, že hladina sa nachádza 8 cm od vrcholu. Po otočení nádoby o 180 stupňov - stojí na vrchole - je hladina vzdialená 2 cm od podstavy. Ako vysoká nádoba je? - Medzi
Medzi 3 stĺpiky je natiahnuté oceľové lanko. Výška prvého stĺpa je 4 m, výška druhého je 3,5m. Vzdialenosť prvých dvoch stĺpikov je 2,5m, vzdialenosť druhího a tretieho je 5m. Päty všetkých troch stĺpikov stojí v jednej priamke. Aká je výška tretieho stĺp - V pravouhlom 5
V pravouhlom trojuholníku je jedna odvesna o 1 m kratšia ako prepona, druhá odvesna je o 2 m kratšia ako prepona. Určite dĺžky všetkých strán trojuholníka. - Rovnobežne cyklista
Pozorovateľ sedí v miestnosti 2 m od okna širokého 50 cm. Rovnobežne vo vzdialenosti 500 m vedie cesta. Akou veľkou priemernou rýchlosťou ide cyklista po tejto ceste, keď ho pozorovateľ vidí 15 s? - Z8–I–5 MO 2019
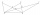Pre osem navzájom rôznych bodov ako na obrázku platí, že body C, D, E ležia na priamke rovnobežnej s priamkou AB, F je stredom úsečky AD, G je stredom úsečky AC a H je priesečníkom priamok AC a BE. Obsah trojuholníka BCG je 12 cm² a obsah štvoruholníka DF - Poklad
Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad. - Polovičná výška
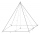Pravidelný štvorboký ihlan má výšku 40 cm a stranu podstavy 21 cm. Ihlan prerežeme v polovičnej výške. Aký veľký objem budú mať obe časti? - Dve tetivy 3
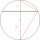Vypočítajte dĺžku tetivy AB a k nej kolmej tetivy BC, ak tetiva AB je od stredu kružnice k vzdialená 4 cm a tetiva BC má vzdialenosť 8 cm. - Tretina kužeľa
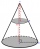Objem pravého kruhového kužeľa je 5 litrov. Vypočítajte objem dvoch častí, na ktoré je kužeľ rozdelený rovinou rovnobežnou so základňou, v jednej tretine vzdialenosti od vrcholu k základni. - MO Z9 2019 domáce kolo
V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC. - Komín
Komín vrhá tieň dlhý 45 metrov. Metrová tyč stojaci kolmo k zemi má tieň dlhý 90 cm. Vypočítaj výšku komína. - Stan a maják
Marcel (bod J) leží v tráve a vidí v zákryte vrchol stanu (bod T) a za ním vrchol majáka (P). |TT'| = 1,2m, |PP'| = 36m, |JT'| = 5m. Marcel leží 15 m odbrehu mora (M). Vypočítajte vzdialenosť majáka od brehu mora – |P'M| .
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
