Úvaha - slovné úlohy a príklady - strana 64 z 112
Počet nájdených príkladov: 2221
- Test 5
 Učitel pripravil test s desiatimi otázkami. Študent má v každej otázke možnosť vybrať jednu správnu odpoveď zo štyroch (A, B,C, D). Študent sa na písomku vôbec nepripravil. Aká je pravdepodobnosť, že: a) Uhádne polovicu odpovedí správne? b) uhádne všetky
Učitel pripravil test s desiatimi otázkami. Študent má v každej otázke možnosť vybrať jednu správnu odpoveď zo štyroch (A, B,C, D). Študent sa na písomku vôbec nepripravil. Aká je pravdepodobnosť, že: a) Uhádne polovicu odpovedí správne? b) uhádne všetky - Výškový uhol
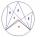 Približne v akej výške je mrak, ktorý vidíme pod výškovým uhlom 26° 10' ak vidíme slnko pod výškovým uhlom 29° 15' a tieň mraku je od nás vzdialený 92 metrov?
Približne v akej výške je mrak, ktorý vidíme pod výškovým uhlom 26° 10' ak vidíme slnko pod výškovým uhlom 29° 15' a tieň mraku je od nás vzdialený 92 metrov? - Poľovníci - hon
 Poľovníci na hone postrieľali rovnaký počet bažantov ako zajacov. Dohromady mali úlovky 408 nôh. Koľko bolo zajacov? (Predpokladajme, že žiadne zviera nebolo handicapované.)
Poľovníci na hone postrieľali rovnaký počet bažantov ako zajacov. Dohromady mali úlovky 408 nôh. Koľko bolo zajacov? (Predpokladajme, že žiadne zviera nebolo handicapované.) - Poľovníci 5638
 Poľovníci ulovili rovnaký počet zajacov a bažantov. Zajace a bažanti mali rovnaký počet nôh. Koľko bolo zajacov?
Poľovníci ulovili rovnaký počet zajacov a bažantov. Zajace a bažanti mali rovnaký počet nôh. Koľko bolo zajacov? - Tohtoročných 5633
 Michalov dedko má 4 vnukov. Pri tohtoročných oslavách zistil, že je 7x starší ako Michal, šesťkrát tak starý ako Vašek, štyrikrát tak starý ako Emil, trikrát tak starý ako Honza. Táto situácia sa môže vyskytnúť iba raz za život. Koľké narodeniny oslavoval
Michalov dedko má 4 vnukov. Pri tohtoročných oslavách zistil, že je 7x starší ako Michal, šesťkrát tak starý ako Vašek, štyrikrát tak starý ako Emil, trikrát tak starý ako Honza. Táto situácia sa môže vyskytnúť iba raz za život. Koľké narodeniny oslavoval - Stovky 2
 Napíšte, koľko je takých dvojcifernych čísel, ktoré ak vynásobíme štyrmi, tak dostaneme výsledok končiaci dvoma nulami.
Napíšte, koľko je takých dvojcifernych čísel, ktoré ak vynásobíme štyrmi, tak dostaneme výsledok končiaci dvoma nulami. - Zásielky 5620
 Ak vieš, že štvrtina postovej zásielky a ešte 300 gramov váži rovnako, ako celá zásielka, potom dve také zásielky vážia koľko gramov?
Ak vieš, že štvrtina postovej zásielky a ešte 300 gramov váži rovnako, ako celá zásielka, potom dve také zásielky vážia koľko gramov? - Z7-1-6 MO 2017
 Vodník Chaluha nalieval hmlu do rozmanitých rôzne veľkých nádob ktoré si starostlivo zoradil na polici. Pri nalievaní postupoval postupne z jednej strany žiadnu nádobu nepreskakoval. Do každej nádoby sa vojde aspoň deciliter hmly. Keby nalieval hmlu sedem
Vodník Chaluha nalieval hmlu do rozmanitých rôzne veľkých nádob ktoré si starostlivo zoradil na polici. Pri nalievaní postupoval postupne z jednej strany žiadnu nádobu nepreskakoval. Do každej nádoby sa vojde aspoň deciliter hmly. Keby nalieval hmlu sedem - Vlak
 Vlak má byť za 10 minút v stanici. Zostáva mu ešte 32 km. Aké bude predpokladané meškani,e ak vlak prejde za 2 minúty 3 km okrem posledného úseku kde jede 2 km za 5 minút.
Vlak má byť za 10 minút v stanici. Zostáva mu ešte 32 km. Aké bude predpokladané meškani,e ak vlak prejde za 2 minúty 3 km okrem posledného úseku kde jede 2 km za 5 minút. - Karolko 2
 Karol si zobral od Ivana 20.februára pôžičku 600 Eur, pri 20% ročnej úrokovej miere. Od Jána 10.mája pôžičku 1100 Eur pri 14% úrokovej miere. Od Milana 15.septembra pôžičku 900 Eur pri 11% úrokovej miere. Všetky tri má vrátiť 30.decembra. Určte, akú mal d
Karol si zobral od Ivana 20.februára pôžičku 600 Eur, pri 20% ročnej úrokovej miere. Od Jána 10.mája pôžičku 1100 Eur pri 14% úrokovej miere. Od Milana 15.septembra pôžičku 900 Eur pri 11% úrokovej miere. Všetky tri má vrátiť 30.decembra. Určte, akú mal d - Elektrina
 Mnohé spoločnosti poskytujúce verejnoprospešné služby podporujú úsporu energie tým, že ponúkajú diskontné sadzby pre spotrebiteľov, ktorí si udržiavajú svoju spotrebu energie pod určitými stanovenými štandardmi. Nedávna správa EPA uvádza, že 70% obyvateľo
Mnohé spoločnosti poskytujúce verejnoprospešné služby podporujú úsporu energie tým, že ponúkajú diskontné sadzby pre spotrebiteľov, ktorí si udržiavajú svoju spotrebu energie pod určitými stanovenými štandardmi. Nedávna správa EPA uvádza, že 70% obyvateľo - Z8-I-6 MO 2017
 Priamka predstavuje číselnú os a vyznačené body zodpovedajú číslam a, −a, a + 1, avšak nie nutne v tomto poradí. Zostrojte body, ktoré zodpovedajú číslam 0 a 1. Preberte všetky možnosti.
Priamka predstavuje číselnú os a vyznačené body zodpovedajú číslam a, −a, a + 1, avšak nie nutne v tomto poradí. Zostrojte body, ktoré zodpovedajú číslam 0 a 1. Preberte všetky možnosti. - Z5–I–1 MO 2017
 Janko dostal vreckové a chce si zaň kúpiť niečo dobré. Keby si kúpil štyri koláče, zvýšilo by mu 0,50 €. Keby si chcel kúpiť päť koláčov, chýbalo by mu 0,60 €. Keby si kúpil dva koláče a tri šišky, utratil by celé vreckové bezo zvyšku. Koľko stojí jedna š
Janko dostal vreckové a chce si zaň kúpiť niečo dobré. Keby si kúpil štyri koláče, zvýšilo by mu 0,50 €. Keby si chcel kúpiť päť koláčov, chýbalo by mu 0,60 €. Keby si kúpil dva koláče a tri šišky, utratil by celé vreckové bezo zvyšku. Koľko stojí jedna š - Z9-I-6 MO 2017
 Na priamke predstavujúcej číselnú os uvážte navzájom rôzne body zodpovedajúce číslam a, 2a, 3a + 1 vo všetkých možných poradiach. Pri každej možnosti rozhodnite, či je také usporiadanie možné. Ak áno, uveďte konkrétny príklad, ak nie, zdôvodnite prečo.
Na priamke predstavujúcej číselnú os uvážte navzájom rôzne body zodpovedajúce číslam a, 2a, 3a + 1 vo všetkých možných poradiach. Pri každej možnosti rozhodnite, či je také usporiadanie možné. Ak áno, uveďte konkrétny príklad, ak nie, zdôvodnite prečo. - Ichtyosaurov 5577
 Na ostrove v Jurskom svete je päť obrovských akvárií. V každom z nich plávajú aspoň dva a najviac šesť ichtyosaurov, pričom v každom akváriu je ich iný počet. Koľko ichtyosaurov je celkom vo všetkých akváriách?
Na ostrove v Jurskom svete je päť obrovských akvárií. V každom z nich plávajú aspoň dva a najviac šesť ichtyosaurov, pričom v každom akváriu je ich iný počet. Koľko ichtyosaurov je celkom vo všetkých akváriách? - Dve kocky 2
 Jana hodí súčasne dvoma hracími kockami. Aká je pravdepodobnosť, že jej padnú v súčte štyri body?
Jana hodí súčasne dvoma hracími kockami. Aká je pravdepodobnosť, že jej padnú v súčte štyri body? - Štvoriciach 5543
 Tanečná skupina sa pripravuje na vystúpenie. programu majú tanca v páre, štvoriciach a päticiach. Koľko členov musí mať skupina, aby mohla tancovať všetky tieto tanca a každého tanca sa zúčastnili všetci jej členovia
Tanečná skupina sa pripravuje na vystúpenie. programu majú tanca v páre, štvoriciach a päticiach. Koľko členov musí mať skupina, aby mohla tancovať všetky tieto tanca a každého tanca sa zúčastnili všetci jej členovia - Záhradníkov 5542
 Traja záhradníci pokosú lúku za určitú dobu. Štyria záhradníci to zvládnu o pol hodiny skôr. Za ako dlho to zvládne päť záhradníkov?
Traja záhradníci pokosú lúku za určitú dobu. Štyria záhradníci to zvládnu o pol hodiny skôr. Za ako dlho to zvládne päť záhradníkov? - Z5–I–6 MO 2017
 Na stole ležalo osem kartičiek s číslami 2,3,5,7,11,13,17,19. Fero si vybral tri kartičky. Sčítal na nich napísané čísla a zistil, že ich súčet je o 1 väčší ako súčet čísel na zvyšných kartičkách. Ktoré kartičky mohli zostať na stole? Určte všetky možnost
Na stole ležalo osem kartičiek s číslami 2,3,5,7,11,13,17,19. Fero si vybral tri kartičky. Sčítal na nich napísané čísla a zistil, že ich súčet je o 1 väčší ako súčet čísel na zvyšných kartičkách. Ktoré kartičky mohli zostať na stole? Určte všetky možnost - Zuzka
 Zuzkin vek bude o 12 rokov štyrikrát väčší, ako bol pred dvanástimi rokmi. Koľko rokov má Zuzka teraz?
Zuzkin vek bude o 12 rokov štyrikrát väčší, ako bol pred dvanástimi rokmi. Koľko rokov má Zuzka teraz?
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
