Delenie + úvaha - príklady a úlohy
Počet nájdených príkladov: 238
- Odmeny - súťaž
Na odmeny pre troch najlepších súťažiacich bola pripravená finančná čiastka v korunách. Prvý súťažiaci získal polovicu tejto sumy. Druhý súťažiaci dostal 300 korún. Tretí súťažiaci získal zvyšok pripravenej čiastky, čo bolo trikrát menej korún, než získal - Na tabuli
Na tabuli bola napísaná úloha na delenie dvoch kladných čísel. Dávid si všimol, že ak delenec zväčší o 2 a deliteľa o 7, podiel sa nezmení. O koľko treba zväčšiť deliteľa, aby pri zväčšení delenca o 3 zasa vyšiel ten istý podiel? - Návštevníci kina
V každom rade letného kina je 35 sedadiel. Urči koľko sa maximálne zmestí do hľadiska návštevníkov, ak vieme že ich je viac ako 705 a menej ako 740. - Orechy - delenie
Koľko najmenej orechov musíme mať aby sme ich podelili medzi 10, 12 a 18 deti?
- Zbierka autíčok
Martin má v zbierke viac ako 50 a menej ako 100 autíčok. pätina z nich sú nákladné autá, osmina veteráni a zvyšok modely súčasných osobných áut. Koľko autíčok má martin v zbierke koľko z nich je osobných áut? - Skupiny
Na aké najväčšie množstvo skupín môžeme rozdeliť 336 detí a 24 dospelých tak, aby bol v každej skupine rovnaký počet detí aj rovnaký počet dospelých? - Žiaci 23
Žiaci deviatých tried boli na exkurzií v takom počte, že si mohli sadnúť k stolom po 4, po 5, po 6 a zakaždým ostalo voľné jedno miesto. Aký je najmenší počet žiakov, ktorí sa exkurzie zúčastnili? - Telocvične
Vo veľkej telocvični sa nachádza 18 baskedbalových lôpt. V malej telocvični je dvakrát menej. Koľko baskedbalových lôpt sa nachádza v malej telocvični? - Rámčeky
Rámař má pripraviť 23 kusov rámčekov na obrázky. Rámček bude mať rozmery 30 cm a 42 cm. Lišty, z ktorých bude rámčeky robiť, majú dĺžku 3 metre. a) Koľko rámčekov urobí z jednej lišty? b) Koľko líšt bude potrebovať?
- Exkurzia - vratka
Z našej triedy sa niekoľko žiakov zúčastnilo na exkurzií. Každý zaplatil rovnakú sumu. Nakoniec zostalo niekoľko eur, ktoré im treba vrátiť. Ak by sme vrátili každému po 3 eurá, zostalo by ešte 5 eur. Ak by sme každému vrátili po 4 eurá, chýbalo by 20 eur - Spravodlivo 4
Vnučka Mia pomahala starkej 3 dní, Ema 2 dní a Zoja 4 dní. V akom pomerne ma starká rozdeliť čokoládu medzi vnučky, ak ich chce spravodlivo odmeniť podľa toho, ako dlho jej pomáhali.? - Traja 44
Traja chlapci Ivo, Vlado a Alan čítajú tú istú knihu, pričom si dal podmienku, že počas celého čítania budú každý deň čítať vždy rovnaký počet strán, až kým knihu nedočítajú do konca. Ivo z nej denne prečíta 18 strán, Vlado 24 strán a Alan 20 strán. Overt - Pokladník 4
Pokladník Samuel mal v pokladni spolu 20 ks bankoviek v celkovej hodnote 850 eur. Boli to iba 50 eurové a 20 eurové bankovky. Koľko kusov mal z každej bankovky? - Centimetroch 82756
Majme kocku ktorej dĺžka hrany vyjadrená v centimetroch je prirodzené číslo. Z akého najmenšieho počtu takých istých kociek je možné vytvoriť kváder s rozmermi 24cm, 32cm a 60 cm. Aká dlhá bude hrana týchto kociek?
- Zajac 2024m
Zajac sa zúčastnil na pretekoch dlhých 2024 metrov. Zo štartovej čiary sa odrazil ľavou nohou a po celý čas pretekov pravidelne striedal ľavú, pravú a obe nohy. Keď sa zajac odrazil ľavou nohou, skočil 35 dm, keď sa odrazil pravou nohou, skočil 15 - Pripravovali 82560
V triediarni ovocie pripravovali z pomarančov a mandarínok ovocné balíčky. Do 35 balíčkov dali rovnaký počet pomarančov aj mandarínok. Do ďalších 25 balíčkov dali iba pomaranče. Počet kusov ovocia bol vo všetkých popísaných balíčkoch rovnaký. Na všetky ba - V Trnave
V Trnave bolo -6 stupňov celsia, koľko bolo v Budapešti, v ktorej bolo dvakrát teplejšie.? - Tanečníkov 82318
Tanečný súbor má 24 členov. Na koľko rovnako veľkých skupín tanečníkov sa môže pri vystúpení rozdeliť_ - Zuzka 7
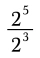Zuzka 8-krát vydelila číslo 52 číslom 2 a 6-krát vynasobila číslom 2. Aké číslo dostala?
Peter s Honzom sa rozhodli, že postavia čo najrýchlejšie stavbu. Za desať minút postavili jednu dvadsatinu stavby. Po 20 minútach sa pridali ďalší traja kamaráti. Všetci stavali rovnakým tempom. Koľko minút trvalo postavenie stavby?Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
