Zlomkový kalkulátor
Kalkulačka provádí základní i pokročilé operace se zlomky, celými čísly, desetinnými čísla a smíšenými čísly. Také zobrazuje podrobní krok za krokem informace o postupu výpočtu. Řešení úloh se dvěma, třemi nebo více zlomky nebo čísly v jednom výrazu.
Výsledek:
1 2/3 × 2 3/4 = 55/12 = 4 7/12 ≅ 4,5833333
Jak jsme vyřešili zlomky krok za krokem?
- Konverze smíšeného čísla 1 2/3 na zlomek: 1 2/3 = 1 2/3 = 1 · 3 + 2/3 = 3 + 2/3 = 5/3
Pokud chcete najít nového čitatele:
a) Vynásobte celé číslo 1 jmenovatelem 3. Celé číslo 1 je totéž jako 1 * 3/3 = 3/3
b) Připočtěte výsledek z předchozího kroku 3 do čitatele 2. Nový čitatel je 3 + 2 = 5
c) Napište předchozí odpověď (nový čitatel 5) nad jmenovatele 3. - Konverze smíšeného čísla 2 3/4 na zlomek: 2 3/4 = 2 3/4 = 2 · 4 + 3/4 = 8 + 3/4 = 11/4
Pokud chcete najít nového čitatele:
a) Vynásobte celé číslo 2 jmenovatelem 4. Celé číslo 2 je totéž jako 2 * 4/4 = 8/4
b) Připočtěte výsledek z předchozího kroku 8 do čitatele 3. Nový čitatel je 8 + 3 = 11
c) Napište předchozí odpověď (nový čitatel 11) nad jmenovatele 4. - Násobení: 5/3 * 11/4 = 5 · 11/3 · 4 = 55/12
Zlomky vynásobíme tak že násobíme čitatele čitatelem a jmenovatele jmenovatelem. Výsledný zlomek zkrátíme největším společným dělitelem NSD(55, 12) = 1. V dalším mezikroku výslední zlomek není možné dále zjednodušit krácením.
Pravidla výrazů se zlomky:
Znak / je zlomková čára, případně znak dělení - napr. 5/100 nebo 1/2 / 3.Smíšené číslo se skládá z celé části a zlomkové části. Zapisujeme jako celé číslo mezera zlomek. Smíšené číslo (smíšený zlomek) se zapíše např. 1 2/3 (jedna a dvě třetiny).
Desetinná čísla se píší s desetinnou tečkou . nebo čárkou , a automaticky se převedou na zlomky - napr. 1,45.
Dvojtečka : znamená dělení, například na dělení smíšených čísel: 1 2/3 : 4 3/8.
Hvězdička * znamená násobení.
Plus + je sčítání, mínus - je odčítání, () {} [] jsou závorky.
Znak umocnění je ^ - použití například: 1/4^3
Příklady použití:
• sčítání zlomků: 2/4 + 3/4• odčítání zlomků: 2/3 - 1/2
• násobení zlomků: 7/8 * 3/9
• dělení zlomků: 1/2 : 3/4
• převrácený zlomek: 1 : 3/4
• druhá mocnina zlomku: 2/3 ^ 2
• třetí mocnina zlomku: 2/3 ^ 3
• umocnění zlomků: 1/2 ^ 4
• umocnění na zlomek: 16 ^ 1/2
• sčítání zlomků a smíšených čísel: 8/5 + 6 2/7
• dělení celého čísla a zlomků: 5 ÷ 1/2
• složený zlomek: 5/8 : 2 2/3
• číslo na zlomek: 0.625
• zlomek na desetinné číslo: 1/4
• zlomek na procenta: 1/8 %
• porovnávaní zlomků: 1/4 2/3
• odmocnina ze zlomku: sqrt(1/16)
• výraz se závorkami: 1/3 * (1/2 - 3 3/8)
• zlomek ze zlomku: 3/4 z 5/7
• násobení: 2/3 z 3/5
• dělením najděte kvocient: 3/5÷2/3
Pořadí operací
Přemýšleli jste někdy nad tím, proč kalkulačky nefungují jen zleva doprava? Tato kalkulačka dodržuje matematické pořadí operací – soubor pravidel, která zajišťují, že každý vypočítá výraz stejným způsobem.
Pravidla pořadí operací
1. Závorky - nejprve vyhodnotíme co je v závorkách.
2. Mocniny nebo exponenty
3. Násobení a dělení,
4. Sčítání a odčítání
Základní pravidla
Pravidlo 1: Násobení a dělení vždy provádíme před sčítáním a odečítáním. Představte si je jako VIP, které přeskočí na začátek řady!
Pravidlo 2: Když mají operace stejnou prioritu (jako například × a ÷ nebo + a −), pracujte zleva doprava - stejně jako při čtení knihy.
Pravidlo 3: Závorky mění přirozené pořadí vyhodnocení operací
Zlomky v slovních úlohách:
- Porce pro psa
 Jana jde jíst k večeři dva párky a Ondřej 4 párky. Přišel zatoulaný pes a dali mu každý po pól párku. Kdo mu dal víc (ve smyslu dal větší podíl ze své porce)?
Jana jde jíst k večeři dva párky a Ondřej 4 párky. Přišel zatoulaný pes a dali mu každý po pól párku. Kdo mu dal víc (ve smyslu dal větší podíl ze své porce)? - Od křižovatky
 Od křižovatky ke škole je 6/5 km, k obchodu 9/10km, k bance 5/8km ak parku 21/8km které místo je ke křižovatce nejblíže?
Od křižovatky ke škole je 6/5 km, k obchodu 9/10km, k bance 5/8km ak parku 21/8km které místo je ke křižovatce nejblíže? - Součet blíže k 1
 Zde jsou dva součty: A = 1/2 + 1/3 a B = 1/5 + 1/3. Která z těchto dvou částek je blíže k 1? Musíte ukázat svou práci a jasně uvést, zda je správná odpověď A nebo B.
Zde jsou dva součty: A = 1/2 + 1/3 a B = 1/5 + 1/3. Která z těchto dvou částek je blíže k 1? Musíte ukázat svou práci a jasně uvést, zda je správná odpověď A nebo B. - Nepravé zlomky
 Jak identifikovat nepravé zlomky? Které z následujících zlomků jsou nepravé? A) 3/4 B) 32/15 C) 3/9 D) 2 2/11
Jak identifikovat nepravé zlomky? Které z následujících zlomků jsou nepravé? A) 3/4 B) 32/15 C) 3/9 D) 2 2/11 - 46% jako zlomek
 Určete správnou odpověď rozumovým uvažováním a výpočtem: Napište 46% jako zlomek. ...
Určete správnou odpověď rozumovým uvažováním a výpočtem: Napište 46% jako zlomek. ... - Srovnání časů závodníků
 Parul a Tarun běžel závod na 200m. Parul dokončil závod za 2/3 minuty a Taun za 3/5 minuty. Kdo si dal víc času?
Parul a Tarun běžel závod na 200m. Parul dokončil závod za 2/3 minuty a Taun za 3/5 minuty. Kdo si dal víc času? - Dělení a násobení zlomků
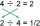 Student ví, že ¾ x 4 je totéž jako 4 x ¾ Student předpokládá, že 4 ÷ ¾ je totéž jako ¾ ÷ 4 Má student pravdu?
Student ví, že ¾ x 4 je totéž jako 4 x ¾ Student předpokládá, že 4 ÷ ¾ je totéž jako ¾ ÷ 4 Má student pravdu?
slovní úlohy - více »
Poslední změna: 17.2.2026
