Solární elektrárna
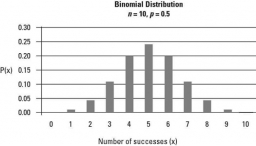
Při výrobě solárních článků se vyrábějí 2% vadných článků. Předpokládejme, že články (buňky) jsou nezávislé a že panel obsahuje 800 buněk. Jaká je přibližná pravděpodobnost, že méně než 20 článků je vadných. (Odpověď s přesností na 3 desetinná místa).
Správná odpověď:
Tipy na související online kalkulačky
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
statistikakombinatorikaÚroveň náročnosti úkolu
Související a podobné příklady:
- Pravděpodobnost 81968
Odborník na výživu, který zkoumá ovoce, uvedl, že průměrná hmotnost maliny je 4,4 g se standardní odchylkou 1,28 g. Jaká je pravděpodobnost, že náhodně vybraná malina by vážila méně než 3,1 gramu? Nechť X představuje hmotnost náhodně vybrané maliny. Předp - Pravděpodobnost 75244
Malý regionální dopravce přijal 12 rezervací na konkrétní let s 11 sedadly. Sedm rezervací šlo běžným zákazníkům, kteří na let dorazí. Každý zbývající cestující dorazí na let se 49% šancí, nezávisle na sobě. (Odpovědi uveďte s přesností na 4 desetinná mís - Předpokládejme 83535
Podle zprávy US Fish and Wildlife Service je průměrná délka šestiletého pstruha duhového v řece Arolik na Aljašce = 484,6 milimetru se standardní odchylkou = 31,2 milimetru. Předpokládejme, že tyto délky jsou normálně rozděleny. Jaký podíl šestiletých pst - Pravděpodobnosti 57683
V dílně se k výrobě židlí používají tři roboty Q, R a S Robot Q tvoří 25% židlí Robot R tvoří 45% židlí Zbývající židle vyrobil Robot S Důkazy ukázaly, že 2 procenta židlí vyrobených robotem Q jsou vadné, 3 procenta židlí vyrobených robotem R a 5 procent - Kelímek sladkostí
V kelímku je 200 sladkostí měřeno s přesností na 10. Váží 600 gramů s přesností na 10 gramů. Jaká je nejmenší možná hmotnost každé sladkosti v gramech? 2 desetinná místa. - Pravděpodobnost 7627
Ve sledované skupině lidí je 8% nemocných chřipkou. Vyšetřilo se 100 lidí z této skupiny. Jaká je pravděpodobnost, že nejvýše 5 z nich bude nemocné chřipkou? (zaokrouhlete na 3 desetinná místa) - Pravděpodobnost 65464
Z 18 lístků, na kterých jsou čísla od 1 po 18, vytáhneme náhodně jeden. Jaká je pravděpodobnost, že na vytaženém lístku bude prvočíslo? Výsledek napište jako desetinné číslo zaokrouhlené na dvě desetinná místa.
