Bernoulli
Pri výrobe solárnych článkov sa vyrábajú 2% chybných článkov. Predpokladajme, že články (bunky) sú nezávislé a že panel obsahuje 800 buniek. Aká je približná pravdepodobnosť, že menej ako 20 článkov je chybných. (odpoveď s presnosťou na 3 desatinné miesta).
Správna odpoveď:
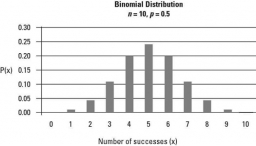
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
štatistikakombinatorikaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Zdravá výživa
Odborník na výživu, ktorý skúma ovocie, uviedol, že priemerná hmotnosť maliny je 4,4 g so štandardnou odchýlkou 1,28 g. Aká je pravdepodobnosť, že náhodne vybraná malina by vážila menej ako 3,1 gramu? Nech X predstavuje hmotnosť náhodne vybranej maliny. P - Pravdepodobnosť 75244
Malý regionálny dopravca prijal 12 rezervácií na konkrétny let s 11 sedadlami. Sedem rezervácií išlo bežným zákazníkom, ktorí na let dorazia. Každý zostávajúci cestujúci dorazí na let so 49% šancou, nezávisle od seba. (Odpovede uveďte s presnosťou na 4 de - Pstruh dúhový
Podľa správy US Fish and Wildlife Service je priemerná dĺžka šesťročného pstruha dúhového v rieke Arolik na Aljaške = 484,6 milimetra so štandardnou odchýlkou = 31,2 milimetra. Predpokladajme, že tieto dĺžky sú normálne rozdelené. Aký podiel šesťročných - Uhádne
Test obsahuje 4 otázky a na každú z nich je 5 rôznych odpovedí, z ktorých je správna len jedna, ostatné sú nesprávne. Aká je pravdepodobnosť, že žiak, ktorý nepozná odpoveď na žiadnu otázku, uhádne správne odpovede na všetky otázky? - Prvočíslo 18
Z 18 lístkov, na ktorých sú čísla od 1 po 18, vytiahneme náhodne jeden. Aká je pravdepodobnosť, že na vytiahnutom lístku bude prvočíslo? Výsledok napíšte ako desatinné číslo zaokrúhlené na dve desatinné miesta. - Výborní a spravodliví
Pri prijímacej skúške na vysokú školu sú účastníci hodnotení ako výborní, veľmi dobrí, dobrí a spravodliví. Zvážte, že skóre v skúške je normálne rozdelené s priemerom 78 a štandardnou odchýlkou 7,5. Účastníci, ktorí získajú prvých 5 % bodov, budú hodno - Chrípka
V sledovanej skupine ľudí je 8% chorých na chrípku. Vyšetrilo sa 100 ľudí z tejto skupiny. Aká je pravdepodobnosť, že najviac 5 z nich bude chorých na chrípku? (zaokrúhlite na 3 desatinné miesta)
