Chrípka
V sledovanej skupine ľudí je 8% chorých na chrípku. Vyšetrilo sa 100 ľudí z tejto skupiny. Aká je pravdepodobnosť, že najviac 5 z nich bude chorých na chrípku?
(zaokrúhlite na 3 desatinné miesta)
(zaokrúhlite na 3 desatinné miesta)
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Hľadáte štatistickú kalkulačku?
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Chceš si dať zrátať kombinačné číslo?
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Chceš si dať zrátať kombinačné číslo?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
štatistikakombinatorikazákladné operácie a pojmyÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Skúšobná komisia
 Podľa komisie pre skúšky z matematiky približne 62 % ľudí, ktorí sa zúčastnili skúšky z matematiky, skúškou uspelo. Ak je náhodne vybraných 18 ľudí, ktorí sa zúčastnili skúšky z matematiky, aká je pravdepodobnosť, že uspelo aspoň 76 %? Zaokrúhlite svoju o
Podľa komisie pre skúšky z matematiky približne 62 % ľudí, ktorí sa zúčastnili skúšky z matematiky, skúškou uspelo. Ak je náhodne vybraných 18 ľudí, ktorí sa zúčastnili skúšky z matematiky, aká je pravdepodobnosť, že uspelo aspoň 76 %? Zaokrúhlite svoju o - Prvočíslo 18
 Z 18 lístkov, na ktorých sú čísla od 1 po 18, vytiahneme náhodne jeden. Aká je pravdepodobnosť, že na vytiahnutom lístku bude prvočíslo? Výsledok napíšte ako desatinné číslo zaokrúhlené na dve desatinné miesta.
Z 18 lístkov, na ktorých sú čísla od 1 po 18, vytiahneme náhodne jeden. Aká je pravdepodobnosť, že na vytiahnutom lístku bude prvočíslo? Výsledok napíšte ako desatinné číslo zaokrúhlené na dve desatinné miesta. - Kábel
 Pretrhol sa telefónny kabel spájajúci miesta A, B vo vzdialenosti 2,5 km. Aká je pravdepodobnosť, že sa to stalo vo vzdialenosti najviac 450 m od miesta A?
Pretrhol sa telefónny kabel spájajúci miesta A, B vo vzdialenosti 2,5 km. Aká je pravdepodobnosť, že sa to stalo vo vzdialenosti najviac 450 m od miesta A? - Bernoulli
 Pri výrobe solárnych článkov sa vyrábajú 2% chybných článkov. Predpokladajme, že články (bunky) sú nezávislé a že panel obsahuje 800 buniek. Aká je približná pravdepodobnosť, že menej ako 20 článkov je chybných. (odpoveď s presnosťou na 3 desatinné miesta
Pri výrobe solárnych článkov sa vyrábajú 2% chybných článkov. Predpokladajme, že články (bunky) sú nezávislé a že panel obsahuje 800 buniek. Aká je približná pravdepodobnosť, že menej ako 20 článkov je chybných. (odpoveď s presnosťou na 3 desatinné miesta - Chrípka
 Za prvý februárový týždeň ochorelo na chrípku 5% deti v škôlke. Druhý týždeň ochorelo ďalších 9 deti, čím počet chorých vzrástol na 20%. Koľko deti chodilo do škôlky?
Za prvý februárový týždeň ochorelo na chrípku 5% deti v škôlke. Druhý týždeň ochorelo ďalších 9 deti, čím počet chorých vzrástol na 20%. Koľko deti chodilo do škôlky? - V kancelárii
 V kancelárii pracuje 100 ľudí. Každý z nich priemerne telefonuje 25 minút denne. Pracovný deň má 8 hodín. Aká je pravdepodobnosť, že bude telefonovať 10 pracovníkov naraz počas jedného dňa?
V kancelárii pracuje 100 ľudí. Každý z nich priemerne telefonuje 25 minút denne. Pracovný deň má 8 hodín. Aká je pravdepodobnosť, že bude telefonovať 10 pracovníkov naraz počas jedného dňa? - Hmotnosť rýb
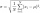 Váhy rýb v určitom jazere je normálne rozdelená s priemerom 11 lb (libier) a štandardnou odchýlkou 6 lb. Ak sú náhodne vybrané 4 ryby, aká je pravdepodobnosť, že priemerná hmotnosť bude medzi 8,6 a 14,6 lb? Vašu odpoveď zaokrúhlite na štvrté desatinné m
Váhy rýb v určitom jazere je normálne rozdelená s priemerom 11 lb (libier) a štandardnou odchýlkou 6 lb. Ak sú náhodne vybrané 4 ryby, aká je pravdepodobnosť, že priemerná hmotnosť bude medzi 8,6 a 14,6 lb? Vašu odpoveď zaokrúhlite na štvrté desatinné m
