Výživa - ovoce
Odborník na výživu, který zkoumá ovoce, uvedl, že průměrná hmotnost maliny je 4,4 g se standardní odchylkou 1,28 g. Jaká je pravděpodobnost, že náhodně vybraná malina by vážila méně než 3,1 gramu?
Nechť X představuje hmotnost náhodně vybrané maliny. Předpokládejme, že rozložení vah je přibližně normální. Najděte P( X < 3,1).
Svou odpověď zaokrouhlete na dvě desetinná místa.
Vaše odpověď:
Nechť X představuje hmotnost náhodně vybrané maliny. Předpokládejme, že rozložení vah je přibližně normální. Najděte P( X < 3,1).
Svou odpověď zaokrouhlete na dvě desetinná místa.
Vaše odpověď:
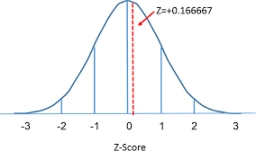
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem aritmetického průměru?
Hledáte statistickou kalkulačku?
Hledáte kalkulačku směrodatné odchylky?
Chceš si dát spočítat kombinační číslo?
Hledáte statistickou kalkulačku?
Hledáte kalkulačku směrodatné odchylky?
Chceš si dát spočítat kombinační číslo?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
statistikakombinatorikaJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Podíl pstruhů pod 446 mm
Podle zprávy US Fish and Wildlife Service je průměrná délka šestiletého pstruha duhového v řece Arolik na Aljašce = 484,6 milimetru se standardní odchylkou = 31,2 milimetru. Předpokládejme, že tyto délky jsou normálně rozděleny. Jaký podíl šestiletých pst - Ryby v jezeře
Váhy ryb v určitém jezeře je normálně rozdělena o průměru 11 lb (liber) a standardní odchylkou 6 lb. Pokud jsou náhodně vybrány 4 ryby, jaká je pravděpodobnost, že průměrná hmotnost bude mezi 8,6 a 14,6 lb? Vaši odpověď zaokrouhlete na čtvrté desetinné mí - Zkušební komise
Podle komise pro zkoušky z matematiky přibližně 62 % lidí, kteří se zúčastnili zkoušky z matematiky, zkouškou uspělo. Pokud je náhodně vybráno 18 lidí, kteří se zúčastnili zkoušky z matematiky, jaká je pravděpodobnost, že uspělo alespoň 76 %? Zaokrouhlete - Životnost cvrčka
Průměrná délka života kriketu je 90 dní se standardní odchylkou 13 dní. Pokud předpokládáme, že životnost kriketu je normálně rozdělena, a. Jaká je pravděpodobnost, že náhodně vybraný cvrček bude mít životnost méně než 75 dní? b. Jaká je pravděpodobnost, - Životnost baterií
Životnost baterií má normální rozložení o průměru 350 minut a standardní odchylkou 10 minut. Jak dlouho vydrží 68% baterií v minutách? Jaká je životnost v minutách, že přibližně 99,7 % baterií vydrží? - Životnost žárovek
Testy ukazují, že životnost žárovek je normálně rozdělena o průměru 750 hodin a standardní odchylkou 75 hodin. Najděte pravděpodobnost, že náhodně vybraná žárovka vydrží 675 až 900 hodin. - Solární elektrárna
Při výrobě solárních článků se vyrábějí 2% vadných článků. Předpokládejme, že články (buňky) jsou nezávislé a že panel obsahuje 800 buněk. Jaká je přibližná pravděpodobnost, že méně než 20 článků je vadných. (Odpověď s přesností na 3 desetinná místa).
