Těleso A-B
Do kvádru o výšce 50 cm se čtvercovou podstavou o hraně délky 20 cm je vyvrtán otvor tvaru válce o průměru 12 cm. Osa tohoto otvoru prochází středy podstav kvádru. Vypočítejte objem a povrch takto vzniklého tělesa.
Vaše odpověď:
Vaše odpověď:
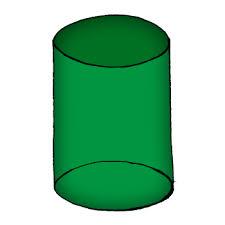
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Čtvercova podstava
Vypočítej povrch jehlanu se čtvercovou podstavou o hraně délky 6 cm a výšce 6 cm. - Rozdíl objemů
Do válce o výšce 10 centimetrů je vložen kvádr se čtvercovou podstavou tak, že jeho podstavava je vepsána do podstavy válce. Hrana podstavy kvádru měří 4 cm. Obě tělesa mají stejnou výšku. Vypočítejte rozdíl objemů válce a kvádru - Hranol + jehlan
Vypočítejte objem tělesa, které je složeno z hranolu a jehlanu se stejnou čtvercovou podstavou o hraně 8 cm. Hranol je vysoký 20 cm a jehlan 15 cm. - Přelití vody z kvádru
Dá se přelít voda z plné nádoby tvaru kvádru o rozměrech 8 cm, 10 cm a 12 cm do nádoby tvaru válce o průměru dna 12 cm a výšce 8 cm? - Povrch kvádru
Máme kvádr se čtvercovou podstavou a výškou 12 dm. Víme, že jeho objem je 588 dm krychlových. Vypočítejte povrch kvádru se stejnou podstavou, ale o 2 cm větší výškou. Výsledek napíšete v dm². - Díra 2
Železný váleček má obvod podstavy 28 π cm. Dělník do válečku z vrchu vyvrtal díru skrz. Po vyvrtání měl daný výrobek o 35% menší objem než před tím. Obvod otvoru v podstave je roven výšce válečku. - Akvárium
Doma máme akvárium tvaru kvádru se čtvercovou podstavou a otec nalil do něj 37 litrů vody. Délka hrany podstavy je 34 cm. Do jaké výšky sahá voda?
