Příklady na jehlan - strana 13 z 15
Počet nalezených příkladů: 293
- Komolý kužel
 Pokud je nádrž zcela plná, nádrž obsahuje 28,54 m³ vody. Průměr horní základny je 3,5 m, zatímco na spodní základně je 2,5 m. Stanovte výšku, pokud je nádrž ve tvaru komolého kužele pravoúhlého kruhového kužele.
Pokud je nádrž zcela plná, nádrž obsahuje 28,54 m³ vody. Průměr horní základny je 3,5 m, zatímco na spodní základně je 2,5 m. Stanovte výšku, pokud je nádrž ve tvaru komolého kužele pravoúhlého kruhového kužele. - Jáma
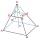 Jáma ve tvaru komolého jehlanu s obdélníkovými podstavami a je hluboká 3,1 m. Délka a šířka jámy je navrchu 3 × 1,5 m, dole 1 m × 0,5 m. Na natření 1 metre čtvereční jámy je třeba 1,4 l zelené barvy. Kolik litrů barvy se na její natření použije, pokud nat
Jáma ve tvaru komolého jehlanu s obdélníkovými podstavami a je hluboká 3,1 m. Délka a šířka jámy je navrchu 3 × 1,5 m, dole 1 m × 0,5 m. Na natření 1 metre čtvereční jámy je třeba 1,4 l zelené barvy. Kolik litrů barvy se na její natření použije, pokud nat - Kulečník
 Vrstva slonovinových kulečníkových koulí o poloměru 6,35 cm, je ve tvaru čtverce. Koule jsou uspořádány tak, že každá koule je tangenty (dotýká se) každé sousedící s ní. V prostorech mezi 4 přilehlými koulemi je prostor rovný velikosti originálu kouli. Po
Vrstva slonovinových kulečníkových koulí o poloměru 6,35 cm, je ve tvaru čtverce. Koule jsou uspořádány tak, že každá koule je tangenty (dotýká se) každé sousedící s ní. V prostorech mezi 4 přilehlými koulemi je prostor rovný velikosti originálu kouli. Po - 2x kužel
 Rotační kužel o výšce 55 cm byl rozříznut rovinou rovnoběžnou s podstavou tak, že vznikl menší rotační kužel a komolý rotační kužel. Objem těchto dvou těles je stejný. Určete výšku menšího kužele.
Rotační kužel o výšce 55 cm byl rozříznut rovinou rovnoběžnou s podstavou tak, že vznikl menší rotační kužel a komolý rotační kužel. Objem těchto dvou těles je stejný. Určete výšku menšího kužele. - Jama 3
 Jáma má tvar pravidelního čtyřbokého komolého jehlanu. Hrany podstav mají délku 14m a 10m. Boční stěny svírají s menší podstavou úhel o velikosti 135°. Určete kolik m³ zeminy bylov ykopano při hloubení jámy?
Jáma má tvar pravidelního čtyřbokého komolého jehlanu. Hrany podstav mají délku 14m a 10m. Boční stěny svírají s menší podstavou úhel o velikosti 135°. Určete kolik m³ zeminy bylov ykopano při hloubení jámy? - Seříznutý kužel
 Horní a dolní poloměr seříznutého pravého kruhového kužele je 8 cm a 32 cm. Je-li výška seříznutého okraje 10 cm, jak daleko od spodní základny musí být vytvořena rovina řezu, aby se vytvořily dva podobné seříznuté kužele?
Horní a dolní poloměr seříznutého pravého kruhového kužele je 8 cm a 32 cm. Je-li výška seříznutého okraje 10 cm, jak daleko od spodní základny musí být vytvořena rovina řezu, aby se vytvořily dva podobné seříznuté kužele? - Komolý kruhový kužel
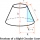 Betonový podstavec má tvar pravoúhlého komolého kruhového kužele s výškou 2,5 metru. Průměr horní a dolní základny je 3 stopy a 5 stop. Určitě boční plochu povrchu, celkovou plochu povrchu a objem podstavce.
Betonový podstavec má tvar pravoúhlého komolého kruhového kužele s výškou 2,5 metru. Průměr horní a dolní základny je 3 stopy a 5 stop. Určitě boční plochu povrchu, celkovou plochu povrchu a objem podstavce. - Jáma - jehlanova
 Jáma má tvar pravidelného seříznutého 4-bokého jehlanu, jejichž podstavné hrany mají velikosti 14m, 10m a hloubka je 6m. Vypočítejte, kolik m³ zeminy bylo při vyhloubení této jámy vyvezeno.
Jáma má tvar pravidelného seříznutého 4-bokého jehlanu, jejichž podstavné hrany mají velikosti 14m, 10m a hloubka je 6m. Vypočítejte, kolik m³ zeminy bylo při vyhloubení této jámy vyvezeno. - Michaela
 Michaela má ve své sbírce dvě vázy. První váza má tvar kužele s průměrem podstavy d = 20 cm; druhá váza má tvar komolého kužele s průměrem spodní podstavy d1 = 25 cm a s průměrem horní podstavy d2 = 15 cm. Do které vázy se vejde více vody, pokud výška obo
Michaela má ve své sbírce dvě vázy. První váza má tvar kužele s průměrem podstavy d = 20 cm; druhá váza má tvar komolého kužele s průměrem spodní podstavy d1 = 25 cm a s průměrem horní podstavy d2 = 15 cm. Do které vázy se vejde více vody, pokud výška obo - Rozdělit řezem
 Daný je kužel s poloměrem podstavy 10 cm a výšce 12 cm. V jaké výšce nad podstavou ho máme rozdělit řezem rovnoběžným s podstavou, aby objemy obou vzniklých teles byly stejné? Výsledek uveďte v cm.
Daný je kužel s poloměrem podstavy 10 cm a výšce 12 cm. V jaké výšce nad podstavou ho máme rozdělit řezem rovnoběžným s podstavou, aby objemy obou vzniklých teles byly stejné? Výsledek uveďte v cm. - Jehlan 6
 Vypočítej povrch a objem pravidelného čtyřbokého komolého jehlanu : a1= 18 cm , a2=6cm /úhel alfa/α=60° (Úhel α je úhel mezi boční stěnou a rovinou podstavy.) S=? , V=?
Vypočítej povrch a objem pravidelného čtyřbokého komolého jehlanu : a1= 18 cm , a2=6cm /úhel alfa/α=60° (Úhel α je úhel mezi boční stěnou a rovinou podstavy.) S=? , V=? - Je dán 21
 Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles.
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - Podstavy
 Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav.
Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav. - Nepodráždil obojek
 Alžbětinský obojek se používá k tomu, aby si zvíře nepodráždilo ránu. Úhel mezi otvorem (průměr 6 palců) a koncem (o průměru 16 palců) svírá se stranou límce úhel 53 stupňů. Najděte uvedenou plochu límce.
Alžbětinský obojek se používá k tomu, aby si zvíře nepodráždilo ránu. Úhel mezi otvorem (průměr 6 palců) a koncem (o průměru 16 palců) svírá se stranou límce úhel 53 stupňů. Najděte uvedenou plochu límce. - Seříznutý kužel
 Objem seříznutého kužele je V=38000π cm³. Poloměr dolní podstavy je o 10 cm větší, než poloměr horní podstavy. Určete poloměr podstav, pokud výška v=60 cm.
Objem seříznutého kužele je V=38000π cm³. Poloměr dolní podstavy je o 10 cm větší, než poloměr horní podstavy. Určete poloměr podstav, pokud výška v=60 cm. - Komolý jehlan
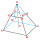 Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů.
Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Komolý jehlan 4
 Betonový podstavec tvaru pravidelného čtyřbokého komolého jehlanu má výšku 12 cm, hrany podstavy mají délky 2,4 a 1,6 dm. Vypočítej povrch podstavce.
Betonový podstavec tvaru pravidelného čtyřbokého komolého jehlanu má výšku 12 cm, hrany podstavy mají délky 2,4 a 1,6 dm. Vypočítej povrch podstavce. - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm. - Strana kužele
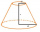 Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°.
Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°. - Komolý jehlan 3
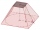 Konvice vysoká 35cm má tvar komolého jehlanu s délkou hrany spodní čtvercové podstavy a=50cm a s hranami obdélníkové podstavy b=20cm a c=30cm. Kolik litru vody se vejde do konvice?
Konvice vysoká 35cm má tvar komolého jehlanu s délkou hrany spodní čtvercové podstavy a=50cm a s hranami obdélníkové podstavy b=20cm a c=30cm. Kolik litru vody se vejde do konvice?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
