Příklady na kužel - strana 10 z 14
Počet nalezených příkladů: 262
- Objemový poměr
Vypočtěte poměr objemů kuliček opsané (poloměr r) a vepsaných (průměr ρ) do rovnostranného rotačního kužele. - Koule v kuželu
Kouli o poloměru 3 cm opište kužel minimálního objemu. Určete jeho rozměry. - Ztrojnásobiť výšku
Jak se změní objem jehlanu, pokud ztrojnásobíme jeho výšku? - Válcová 7
Válcová tyč o průměru 6 cm a délka 20 cm se má obrousit tak, aby vznikla kuželovitá tyčinka o stejné délce a stejném průměru podstavy . Jaký bude objem odstraněného materiálu? - Poloměr podstavy
Jak se změní objem rotačního kužele, pokud: a) zdvojnásobíme poloměr podstavy b) 3 krát zmenšíme výšku c) 5 krát zmenšíme poloměr podstavy - Koule a kužel
Do koule o poloměru G = 36 cm vepište kužel s největším objemem. Jaký je tento objem a jaké jsou rozměry kužele? - Do rovnostranného 2
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Divnej kužel
Rotační kužel má výšku 72cm a úhel při vrcholu 72°. Určete objem koule se stejným poloměrem jako kužel. - Úhel
Objem rotačního kužele je 9,42 cm3, přičemž výška je rovna 10 cm. Jaký úhel svírá strana kužele s rovinnou podstavy? - Výška 13
Výška 9cm průměr 24cm kužel - vypočítej jeho objem a povrch. - Postavy 64744
Kužel vysoký 12 cm a poloměr postavy je 9cm. Zjisti jeho povrch. - Koule
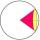Průnik roviny a koule je kruh s poloměrem 60mm. Kužel, jehož podstavou je tento kruh a jehož vrchol leží ve středu koule má výšku 34mm. Vypočítejte povrch a objem koule. - Centimetrech 46001
Vyjádři ve čtverečních centimetrech povrch koule, jejíž poloměr se rovná jedné čtvrtině poloměru kužele. Průměr podstavy kužele je 20cm - Trojúhelník - plášť
Které z tvrzení není správné: ... - Max - kužel
Ze železné tyče ve tvaru hranolu o rozměrech 12 cm, 10,9 cm, 8,5 cm je třeba vyrobit co největší kužel. a) Vypočtěte jeho objem. b) Vypočtěte odpad. - Komolý kužel
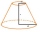Kužel s poloměrem podstavy 12 cm a výškou 20 cm byl ve vzdálenosti 6 cm od podstavy seříznutý, čímž vznikl komolý kužel. Zjistěte poloměr podstavy komolého kužele. - Ze železné
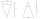Ze železné tyče ve tvaru hranolu o rozměrech 5,6 cm 4,8 cm, 7,2 cm je třeba vyrobit co největší kužel. a) Vypočtěte jeho objem. b) Vypočtěte odpad. - Komolý jehlan
Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm. - Miško
Miško vymodeloval z plastelíny 15 cm vysoký jehlan s obdélníkovou podstavou se stranami podstavy a = 12 cm a b = 8 cm. Janka z tohoto jehlanu vymodelovala rotační kužel s průměrem podstavy d = 10 cm. Jakou výšku měl Jankin kužel? - Přesýpací hodiny
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
