Matematická olympiáda - příklady - strana 5 z 11
Počet nalezených příkladů: 207
- Rok 2018 jak číslo
Součin tří kladných čísel je 2018. Která jsou to čísla? - C – I – 6 MO 2018
Najděte všechna trojmístná čísla n s třemi různými nenulovými číslicemi, která jsou dělitelná součtem všech tří dvojmístných čísel, jež dostaneme, když v původním čísle vyškrtneme vždy jednu číslici. - Trojúhelníku 7247
Na straně AB trojúhelníku ABC jsou dány body D a E tak, že |AD| = |DE| = |EB|. Body A a B jsou postupně středy úseček CF a CG. Přímka CD protíná přímku FB v bodě I a přímka CE protíná přímku AG v bodě J. Dokažte, že průsečík přímek AI a BJ leží na přímce - Z5 – I – 2 MO 2018
Tereza dostala čtyři shodné pravoúhlé trojúhelníky se stranami délek 3 cm, 4 cm a 5 cm. Z těchto trojúhelníků (ne nutně ze všech čtyř) zkoušela skládat nové útvary. Postupně se jí podařilo složit čtyřúhelníky s obvodem 14 cm, 18 cm, 22 cm a 26 cm, a to po - Z6-I-6 MO 2018
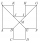Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct - Z7–I–2 MO 2018 Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M. Čtyřúhelník ABMJ m
- Z7–I–5 MO 2018
V zahradnictví Rose si jedna prodejna objednala celkem 120 růží v barvě červené a žluté, druhá prodejna celkem 105 růží v barvě červené a bílé a třetí prodejna celkem 45 růží v barvě žluté a bílé. Zahradnictví zakázku splnilo, a to tak, že růží stejné bar - Z7-1-6 MO 2018
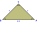Je dán rovnoramenný pravoúhlý trojúhelník ABS se základnou AB. Na kružnici, která má střed v bodě S a prochází body A a B, leží bod C tak, že trojúhelník ABC je rovnoramenný. Určete, kolik bodů C vyhovuje uvedeným podmínkám, a všechny takové body sestrojt - Z6-1-4 MO 2018
Pan Petřík má na zahradě 3 trpaslíky. Největší je Mašík, prostřední Jířa a nejmenší Faltýnek. Když postaví Faltýnka na Jířu jsou stejně vysocí jako Mašík. Když postaví Faltýnka na Mašíka měří o 34 cm více než Jířa. Když postaví na Mašíka Jířu, jsou o 72 c - Z6–I–1 MO 2018
Ivan a Mirka se dělili o hrušky na míse. Ivan si bere dvě hrušky a Mirka polovinu toho co na míse zbývá. Takto postupně odebírali Ivan, Mirka, Ivan, Mirka a nakonec Ivan, který vzal poslední dvě hrušky. Určete, kdo měl nakonec víc hrušek a o kolik. - Z9 – I – 5 MO 2018
Adam a Eva vytvářeli dekorace z navzájem shodných bílých kruhů. Adam použil čtyři kruhy, které sestavil tak, že se každý dotýkal dvou jiných kruhů. Mezi ně pak vložil jiný kruh, který se dotýkal všech čtyř bílých kruhů, a ten vybarvil červeně. Eva použila - MO C–I–1 2018 Neznámé číslo je dělitelné právě čtyřmi čísly z množiny {6, 15, 20, 21, 70}. Určete, kterými.
- Matematická 7136
Z 50 žáků 44 řešilo alespoň jednu z olympiád - MO matematická olympiáda, BO biologická olympiáda. MO neřešilo 20 žáků. Těch, co řešili obě olympiády, byla 1/3 z těch, co řešili právě jednu olympiádu. Kolik žáků řešilo jen MO, jen BO? Kolik řešilo MO i BO - Když bude
Když bude Bedřichovi tolik let, co má Adam dnes, bude mít Adam 14 let. Když bude Adamovi tolik let, kolik má Bedřich dnes, měl Bedřich dva roky. Kolik let má dnes Adam a Bedřich? - MO Z8-I-1 2018 Ferda a David se denně potkávají ve výtahu. Jednou ráno zjistili, že když vynásobí své současné věky, dostanou 238. Kdyby totéž provedli za čtyři roky, byl by tento součin 378. Určete součet současných věků Ferdy a Davida.
- MO Z9-I-3 2018
V našem městě jsou tři kina, kterým se říká podle světových stran. O jejich otevíracích dobách je známo, že: • každý den má otevřeno alespoň jedno kino, • pokud má otevřeno jižní kino, potom nemá otevřeno severní kino, • nikdy nemá otevřeno současně sever - Z5–I–1 MO 2018
Míša má pět pastelek. Vojta jich má méně než Míša. Vendelín jich má tolik, kolik Míša a Vojta dohromady. Všichni tři dohromady mají sedmkrát více pastelek, než má Vojta. Kolik pastelek má Vendelín? - Z8-I-2 MO 2018
Do třídy přibyl nový žák, o kterém se vědělo, že kromě angličtiny umí výborně ještě jeden cizí jazyk. Tři spolužáci se dohadovali, který jazyk to je. První soudil: „Francouzština to není. " Druhý hádal: „Je to španělština nebo němčina. " Třetí usuzoval: „ - Z5–I–4 MO 2018
V klubovně byly jen židle a stůl. Každá židle měla čtyři nohy, stůl byl trojnohý. Do klubovny přišli skauti. Každý si sedl na svou židli, dvě židle zůstaly neobsazené a počet nohou v místnosti byl 101. Kolik židlí bylo v klubovně? - Z7–I–1 MO 2018
Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné číslo poskládané z těchto kartiček je dělitelné šesti. Navíc lze z těchto kartiček poskládat trojmístné číslo
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám tenhle příklad a my Ti ho zkusíme vypočítat.
