Matematická olympiáda - příklady - strana 6 z 11
Počet nalezených příkladů: 207
- Z9 – I – 6 2018 MO
Přirozené číslo N nazveme bombastické, pokud neobsahuje ve svém zápise žádnou nulu a pokud žádné menší přirozené číslo nemá stejný součin číslic jako číslo N. Karel se nejprve zajímal o bombastická prvočísla a tvrdil, že jich není mnoho. Vypište všechna d - Z7–I–4 2018 MO Betka
Karel si hrál s ozubenými koly, která byla sestavena do soukolí. Když zatočil jedním kolem, točila se všechna ostatní. První kolo mělo 32 a druhé 24 zubů. Když se třetí kolo otočilo (je uprostřed soukolí) přesně osmkrát, druhé kolo udělalo pět otáček a čá - MO Z8–I–5 - 2018
Král dal zedníku Václavovi za úkol postavit zeď silnou 25 cm, dlouhou 50 m a vysokou 2 m. Pokud by Václav pracoval bez přestávky a stejným tempem, postavil by zeď za 26 hodin. Podle platných královských nařízení však musí Václav dodržovat následující podm - MO Z8–I–6 2018
V lichoběžníku KLMN má základna KL velikost 40 cm a základna MN má velikost 16 cm. Bod P leží na úsečce KL tak, že úsečka NP rozděluje lichoběžník na dvě části se stejnými obsahy. Určete velikost úsečky KP. - Z9–I–1 2018 čísla
Najděte všechna kladná celá čísla x a y, pro která platí: 1/x + 1/y = 1/4 - Z7-1-3 MO 2018
Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta - Z9-I-4 2018 Hoteliér
Hoteliér chtěl vybavit jídelnu novými židlemi. V katalogu si vybral typ židle. Až při zadávání objednávky se od výrobce dozvěděl, že v rámci slevové akce nabízejí každou čtvrtou židli za poloviční cenu a že tedy oproti plánu může ušetřit za sedm a půl žid - Z9 – I – 2 MO 2018
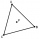V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM. - Cifra
Jaké je poslední číslo 2016-té mocniny čísla 2017? - Obdélníky 6598
Adam měl tři shodné obdélníky. Přiložil je k sobě a dostal obdélník s obvodem 50 cm. Potom je přiložil jinak a dostal obdélník s větším obvodem. Vypoctej jeho obvod. - Z bodu
Z bodu A do B je to 16 km z bodu C do B je to 20 km z bodu C do D je to 19 km kolik kilometru to je z bodu D do bodu A - C–I–4 MO 2017
Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla. - Rychlostí 5874
Mišo a Rišo běhali po běžecké dráze tam a zpět. Rozjeli se proti sobě, každý z jiného konce dráhy. Oba stále běželi stejnou rychlostí, každý jinou. Poprvé se setkali 800 m od jednoho konce dráhy, podruhé na druhém konci dráhy. Jakou délku má běžecká dráha - MO Z6-1-3 2017 šachovnica
Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H - Z7-I-5 MO 2017
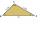Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom - Z7-1-6 MO 2017
Vodník Chaluha naléval mlhu do rozmanitých, různě velkých nádob, které si pečlivě seřadil na polici. Při nalévání postupoval postupně z jedné strany, žádnou nádobu nepřeskakoval. Do každé nádoby se vejde alespoň decilitr mlhy. Kdyby naléval mlhu sedmilitr - Z8-I-6 MO 2017
Přímka představuje číselnou osu a vyznačené body odpovídají číslům a, - a, a + 1, avšak v neurčeném pořadí. Sestrojte body, které odpovídají číslům 0 a 1. Proberte všechny možnosti. - Z9-I-6 MO 2017
Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč. - Z5–I–6 MO 2017
Na stole leželo osm kartiček s čísly 2, 3, 5, 7, 11, 13, 17, 19. Ferda si vybral tři kartičky. Sečetl na nich napsaná čísla a zjistil, že jejich součet je o 1 větší než součet čísel na zbylých kartičkách. Které kartičky mohly zůstat na stole? Určete všech - Z7-I-4 MO 2017
Na stole leželo šest kartiček s ciframi 1, 2, 3, 4, 5, 6. Anežka z těchto kartiček složila šestimístné číslo, které bylo dělitelné šesti. Potom postupně odebírala kartičky zprava. Když odebrala první kartičku, zůstalo na stole pětimístné číslo dělitelné p
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
