Matematická olympiáda - příklady - strana 7 z 11
Počet nalezených příkladů: 207
- Z9-I-5 MO 2017 obdélník
Uvnitř obdélníku ABCD leží body E a F tak, že úsečky EA, ED, EF, FB, FC jsou navzájem shodné. Strana AB je dlouhá 22 cm a kružnice opsaná trojúhelníku AFD má poloměr 10cm. Určete délku strany BC. - Z9–I–4 MO 2017
Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p - Bonbóny MO Z6-I-5 2017
V plechovce byly červené a zelené bonbóny. Čeněk snědl 2/5 všech červených bonbónů a Zuzka snědla 3/5 všech zelených bonbónů. Teď tvoří červené bonbóny 3/8 všech bonbónů v plechovce. Kolik nejméně bonbónů mohlo být původně v plechovce? - MO Z6 I-3 2017 sklenice
Honza měl 100 stejných zavařovacích sklenic, z kterých si stavěl trojboké pyramidy. Nejvyšší poschodí pyramidy má vždy jednu sklenici, druhé poschodí shora představuje rovnostranný trojúhelník, jehož strana sestává ze dvou sklenic, atd. Příklad konstrukce - Z7–I–2 MO 2017
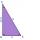Jsou dány dvě dvojice rovnoběžných přímek AB k CD a AC k BD. Bod E leží na přímce BD, bod F je středem úsečky BD, bod G je středem úsečky CD a obsah trojúhelníku ACE je 20 cm². Určete obsah trojúhelníku DFG. - MO Z7–I–3 2017
Zoologická zahrada nabízela školním skupinám výhodné vstupné: každý pátý žák dostává vstupenku zdarma. Pan učitel 6.A spočítal, že pokud koupí vstupné dětem ze své třídy, ušetří za čtyři vstupenky a zaplatí 1 995 Kč. Paní učitelka 6.B mu navrhla, ať koupí - MO Z8–I–4 2017
Roboti Robert a Hubert skládají a rozebírají kafemlýnky. Přitom každý z nich kafemlýnek složí čtyřikrát rychleji, než jej ten druhý rozebere. Když ráno přišli do dílny, několik kafemlýnků už tam bylo složeno. V 9:00 začal Hubert skládat a Robert rozebírat - Hodiny 11
Matěj zjišťoval, jak přesně měří věžní hodiny čas. Došel k závěru, že kdyby je nikdo průběžně nenastavoval, ukazovali by zcela přesný čas vždy jednou za 200 dnů. a) Vypočítej, o kolik sekund se čas měřený věžními hodinami liší od přesného času za 1 hodinu - Z8-I-2 MO 2017
V ostroúhlém trojúhelníku KLM má úhel KLM velikost 68°. Bod V je průsečíkem výšek a P je patou výšky na stranu LM. Osa úhlu P V M je rovnoběžná se stranou KM. Porovnejte velikosti úhlů MKL a LMK. - MO Z6–I–1 - 2017 - Anička
Anička a Blanka si napsaly každá jedno dvojmístné číslo, které začínalo sedmičkou. Dívky si zvolily různá čísla. Poté každá mezi obě číslice vložila nulu, takže jim vzniklo trojmístné číslo. Od něj každá odečetla svoje původní dvojmístné číslo. Výsledek j - MO Z6-I-2 2017
Erika chtěla nabídnout čokoládu svým třem kamarádkám. Když ji vytáhla z batohu, zjistila, že je polámaná jako na obrázku. (Vyznačené čtverečky jsou navzájem shodné.) Dívky se dohodly, že čokoládu dále lámat nebudou a losem určí, jak velký kousek která dos - MO Z8–I–3 - 2017 - Adélka
Adélka měla na papíře napsána dvě čísla. Když k nim připsala ještě jejich největší společný dělitel a nejmenší společný násobek, dostala čtyři různá čísla menší než 100. S úžasem zjistila, že když vydělí největší z těchto čtyř čísel nejmenším, dostane nej - Z9–I–3 - 2017 kafemlýnky2 Roboti Robert a Hubert skládají a rozebírají kafemlýnky. Přitom každý z nich kafemlýnek složí čtyřikrát rychleji, než jej sám rozebere. Když ráno přišli do dílny, několik kafemlýnků už tam bylo složeno. V 7:00 začal Hubert skládat a Robert rozebírat, přes
- MO Z9–I–1 2017
Věkový průměr všech lidí na oslavě byl roven počtu přítomných. Po odchodu jedné osoby, které bylo 29 let, byl věkový průměr zase roven počtu přítomných. Kolik lidí bylo původně na oslavě? - Jeníček 5385
Jeníček dostal kapesní a chce si za něj koupit něco dobrého. Kdyby si koupil čtyři koláče, zvýšilo by mu 0,50 €. Kdyby si chtěl koupit 5 koláčů, chybělo by mu 0,60 EUR. Kdyby si koupil dva koláče a tři koblihy, utratil by celé kapesné beze zbytku. Kolik s - MO8-Z8-I-5 2017
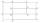Shodné obdélníky ABCD a EFGH jsou umístěny tak, že jejich shodné strany jsou rovnoběžné. Body I, J, K, L, M a N jsou průsečíky prodloužených stran jako na obrázku. Obsah obdélníku BNHM je 12 cm2, obsah obdélníku MBCK je 63 cm² a obsah obdélníku - Z8–I–1 2017 Číslo milion
Vyjádřete číslo milion (1000000) pomocí čísel obsahujících pouze číslice 9 a algebraických operací plus, minus, krát, děleno, mocnina a odmocnina. Určete alespoň tři různá řešení. - Matematické 5319
V matematické soutěži řešili její účastníci dva úkoly. Každý vyřešil alespoň jednu úlohu, přitom první úlohu vyřešilo 80 % účastníků, druhou úlohu 50 %. Obě úkoly vyřešilo 60 účastníků. Kolik účastníků měla soutěž? - MO C - 2017 Najděte nejmenší čtyřmístné číslo abcd takové, že rozdíl (ab)2−(cd)2 je trojmístné číslo zapsané třemi stejnými číslicemi.
- Hodinář
Starý hodinář má ve své sbírce zvláštní digitální budík, který zvoní vždy, když součet cifer, který budík ukazuje, se rovná číslu 21. Zjisti, ve kterých časech bude budík zvonit. Jaký je jejich počet? Vypiš všechny možnosti ...
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám tenhle příklad a my Ti ho zkusíme vypočítat.
