MO C - 2017
Najděte nejmenší čtyřmístné číslo abcd takové, že rozdíl (ab)2−(cd)2 je trojmístné číslo zapsané třemi stejnými číslicemi.
Správná odpověď:
Zobrazuji 1 komentář:
Teacher
Najděte nejmenší čtyřmístné číslo abcd takové, že rozdíl (ab)2−(cd)2 je trojmístné číslo zapsané třemi stejnými číslicemi.
Pomocí vzorce (a - b) (a + b) = (a2 - b2) můžeme rozdíl (ab)2 − (cd)2 přepsat jako (ab + cd) (ab - cd). Protože rozdíl je trojciferný, musí být ab + cd a ab - cd obě dvouciferná. Zároveň musí platit ab > cd. Nejmenší možné hodnoty jsou tedy ab + cd = 101 a ab - cd = 11. Řešením soustavy rovnic jsou hodnoty ab = 56 a cd = 45. Nejmenší čtyřmístné číslo splňující podmínku je tedy 5645.
Přeji pěkný den!
Pomocí vzorce (a - b) (a + b) = (a2 - b2) můžeme rozdíl (ab)2 − (cd)2 přepsat jako (ab + cd) (ab - cd). Protože rozdíl je trojciferný, musí být ab + cd a ab - cd obě dvouciferná. Zároveň musí platit ab > cd. Nejmenší možné hodnoty jsou tedy ab + cd = 101 a ab - cd = 11. Řešením soustavy rovnic jsou hodnoty ab = 56 a cd = 45. Nejmenší čtyřmístné číslo splňující podmínku je tedy 5645.
Přeji pěkný den!
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikazákladní operace a pojmyčíslatémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Římská čísla +
Sečtěte daná čísla zapsané římskými číslicemi. Výsledky zapište jako dekadické číslo. - Dělitelné 83673
Najděte nejmenší kladné celé číslo n takové, že n! je dělitelné 75. - Římská čísla 2+ Sečtěte daná čísla zapsané římskými číslicemi. Výsledky zapište římskými číslicemi.
- Neznámé číslo
Neznámé číslo je dělitelné právě třemi různými prvočísly. Když tato prvočísla srovnáme vzestupně, platí následující: • Rozdíl druhého a prvního prvočísla je polovinou rozdílu třetího a druhého prvočísla. • Součin rozdílu druhého a prvního prvočísla s rozd - Pro čtyřmístné
Pro čtyřmístné číslo abcd platí, že ab: bc = 1:3 a bc: cd = 2:1 (ab, bc a cd jsou dvojmístná čísla z cifer a, b, c, d). Určete toto číslo. - Čtyřmístné číslo
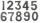Najdi takové čtyřmístné číslo, jehož čtyřnásobek napsaný odzadu, je totéž číslo. - Vynásobím 5847
Neznámé číslo zmenším o 5 a výsledný rozdíl vynásobím třemi. Nakonec výsledný součin zvětším o 6 a dostanu nejmenší společný násobek čísel 3 a 8. Vypočítej neznámé číslo.
