Matematická olympiáda - příklady - strana 4 z 11
Počet nalezených příkladů: 207
- MO Z9-I-6 2019
Kristýna zvolila jisté liché přirozené číslo dělitelné třemi. Jakub s Davidem pak zkoumali trojúhelníky, které mají obvod v milimetrech roven Kristýnou zvolenému číslu a jejichž strany mají délky v milimetrech vyjádřeny navzájem různými celými čísly. Jaku - Z8–I–3 MO 2019
Vendelín bydlí mezi dvěma zastávkami autobusu, a to ve třech osminách jejich vzdálenosti. Dnes vyrazil z domu a zjistil, že ať by utíkal k jedné, nebo druhé zastávce, dorazil by na zastávku současně s autobusem. Průměrná rychlost autobusu je 60 km/h. Jako - Z9 – I – 1 MO 2019
Ondra, Matěj a Kuba se vracejí ze sbírání ořechů, celkem jich mají 120. Matěj si stěžuje, že Ondra má jako vždy nejvíc. Otec přikáže Ondrovi, aby přisypal ze svého Matějovi tak, aby mu počet ořechů zdvojnásobil. Nyní si stěžuje Kuba, že nejvíc má Matěj. N - MO 2019 Z9–I–5
Majka zkoumala vícemístná čísla, ve kterých se pravidelně střídají liché a sudé číslice. Ta, která začínají lichou číslicí, nazvala komická a ta, která začínají sudou číslicí, nazvala veselá. (Např. Číslo 32387 je komické, číslo 4529 je veselé. ) Majka vy - Gramáže v kuchařce (Matik)
V kuchařce od Matěje Matemakaka se psalo: největší společný dělitel gramáže mouky a gramáže cukru je 15, největší společný dělitel gramáže cukru a gramáže citronové kůry je 6, součin gramáže cukru a gramáže citrónové kůry je 1800, nejmenší společný násobe - V Kocourkově - Z8-I-6 2019 MO
V Kocourkově používají mince pouze se dvěma hodnotami, které jsou vyjádřeny v kocourkovských korunách kladnými celými čísly. Pomocí dostatečného množství takových mincí je možné zaplatit jakoukoli celočíselnou částku větší než 53 kocourkovských korun, a t - Richardove čísla Z8-I-2 2019
Richard si pohrával s dvěma pětimístnými čísly. Každé sestávalo z navzájem různých číslic, které u jednoho byly všechny liché a u druhého všechny sudé. Po chvíli zjistil, že součet těchto dvou čísel začíná dvojčíslím 11 a končí číslem 1 a že jejich rozdíl - MO Z8-I-2 2012
Číslo X je nejmenší takové přirozené číslo, jehož polovina je dělitelná třemi, třetina dělitelná čtyřmi, čtvrtina dělitelná jedenácti a jeho polovina dává zbytek 5 po dělení sedmi. Najděte toto číslo. - MO Z9 2019 domace kolo V trojúhelníku ABC leží bod P ve třetině úsečky AB blíže bodu A, bod R je ve třetině úsečky P B blíže bodu P a bod Q leží na úsečce BC tak, že úhly P CB a RQB jsou shodné. Určete poměr obsahů trojúhelníků ABC a PQC.
- MO C-I-3 2019 Určete všechny dvojice přirozených čísel A a B, pro které platí, že součet dvojnásobku nejmenšího společného násobku a trojnásobku největšího společného dělitele přirozených čísel A a B je roven jejich součinu.
- Z9–I–3 MO 2019
Pro která celá čísla x je podíl (x+11)/(x+7) celým číslem? Najděte všechna řešení. - MO B 2019 ukol 2 Přirozené číslo n má aspoň 73 dvojmístných dělitelů. Dokažte, že jedním z nich je číslo 60. Uveďte rovněž příklad čísla n, které má právě 73 dvojmístných dělitelů, včetně náležitého zdůvodnění.
- Dva přátele
Dva přátele cestující letadlem měli dohromady 35 kg zavazadel. Za nadváhu při přepravě zaplatil jeden 72 korun a druhý 108 korun. Kdyby za všechna zavazadla platil jen jeden, stálo by ho to 300 korun. Jakou hmotnost zavazadel měl každý z nich, kolik kilog - Samopočet
Samopočet funguje přesně jako kalkulačka. Hostinský chtěl na samopočte sečíst několik trojmístných přirozených čísel. Na první pokus dostal výsledek 2224. Pro kontrolu sečetl tato čísla znovu a vyšlo mu 2198. Proto sečetl tato čísla ještě jednou a nyní do - Prvočísla - 6c
Najít všechna šesticiferná prvočísla, která obsahují každou z číslic 1,2,4,5,7 a 8 právě jednou. Kolik jich je? - MO Z6–I–3 2018
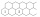Na obrazku jsou naznačeny dvě řady šestiúhelníkových pole které doprava pokračují bez omezení do každého pole doplňte jedno kladné celé číslo tak aby součet čísel v libovolných třech navzájem sousedících polích byl 2018. Určete číslo které bude 2019 políč - C – I – 3 MO 2018
Nechť a, b, c jsou kladná reálná čísla, jejichž součet je 3, a každé z nich je nejvýše 2. Dokažte, že platí nerovnost: a2 + b2 + c2 + 3abc < 9 - Z6–I–5 MO 2018 V následujícím příkladě na sčítání představují stejná písmena stejné číslice, různá písmena různé číslice. RATAM RAD -------------- ULOHY
- MO Z8 – I – 4 2018 Na čtyřech kartičkách byly čtyři různé číslice, z nichž jedna byla nula. Vojta z kartiček složil co největší čtyřmístné číslo, Martin pak co nejmenší čtyřmístné číslo. Adam zapsal na tabuli rozdíl Vojtova a Martinova čísla. Potom Vojta z kartiček složil c
- Z5 – I – 5 Tomáš dostal devět kartiček, na nichž byly následující čísla a matematické symboly: 18, 19, 20, 20, +, −, ×, (, ) Kartičky skládal tak, že vedle sebe nikdy neležely dvě kartičky s čísly, tj. Střídaly se kartičky s čísly a kartičky se symboly. Takto vznikl
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
