Objem - slovní úlohy a příklady - strana 107 z 118
Počet nalezených příkladů: 2347
- Zahradní jezírko
 Betonové zahradní jezírko má dno tvaru půlkruhu o průměru 1,8 m a je 57 cm hluboké. Tatínek ho chce vykachličkovat. Kolik litrů vody bude v jezírku, naplníme-li jej do výšky 17 cm ?
Betonové zahradní jezírko má dno tvaru půlkruhu o průměru 1,8 m a je 57 cm hluboké. Tatínek ho chce vykachličkovat. Kolik litrů vody bude v jezírku, naplníme-li jej do výšky 17 cm ? - Železná koule
 Železná koule má hmotnost 100 kg, hustota ρ = 7600 kg/m³. Vypočítejte objem, povrch a průměr koule.
Železná koule má hmotnost 100 kg, hustota ρ = 7600 kg/m³. Vypočítejte objem, povrch a průměr koule. - Valcová nádoba
 Do válcové nádoby vlily 3,5 litru vody. Pokud měla nádoba průměr podstavy 3 dm, voda sahala přibližně do jaké výšky?
Do válcové nádoby vlily 3,5 litru vody. Pokud měla nádoba průměr podstavy 3 dm, voda sahala přibližně do jaké výšky? - Kvádr akvárium
 Kvádr 25 na 30 centimetrů. Kolik má další stana, pokud tam má vejít 30 l vody?
Kvádr 25 na 30 centimetrů. Kolik má další stana, pokud tam má vejít 30 l vody? - Koule v kuželu
 Kouli o poloměru 3 cm opište kužel minimálního objemu. Určete jeho rozměry.
Kouli o poloměru 3 cm opište kužel minimálního objemu. Určete jeho rozměry. - Kužel
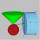 Do rotačního kužele o rozměrech r = 8 cm, v = 8 cm vepište válec maximálního objemu tak, aby osa válce byla kolmá na osu kužele. Určete rozměry válce.
Do rotačního kužele o rozměrech r = 8 cm, v = 8 cm vepište válec maximálního objemu tak, aby osa válce byla kolmá na osu kužele. Určete rozměry válce. - Valec
 Objem válce je 3,5 litra. Obsah podstavy 1,9 decimetru čtvěrečního. Vypočtěte výšku válce.
Objem válce je 3,5 litra. Obsah podstavy 1,9 decimetru čtvěrečního. Vypočtěte výšku válce. - Spotřeba auta
 Auto má spotřebu 6,2 l/100 km. Kolik peněz mě bude stát cesta, při které najedu 410 km při ceně nafty 1,72 USD/l?
Auto má spotřebu 6,2 l/100 km. Kolik peněz mě bude stát cesta, při které najedu 410 km při ceně nafty 1,72 USD/l? - Vodojem
 Ve vodojemu tvaru kvádru je 2000 hl vody, výška vody je 2,5 m. Určete rozměry dna, pokud jeden rozměr je o 3,1 m větší, než druhý.
Ve vodojemu tvaru kvádru je 2000 hl vody, výška vody je 2,5 m. Určete rozměry dna, pokud jeden rozměr je o 3,1 m větší, než druhý. - Dělníci
 Dělníci kopou na školním dvoře jámu na doskočiště. Jáma má tvar kvádru s délkou 19 m, šířkou 20 dm a hloubkou 36 cm. Za hodinu vykopou 0,4 m³ zeminy. Kolik času (hodin a minut) potřebují na vyhloubení jámy?
Dělníci kopou na školním dvoře jámu na doskočiště. Jáma má tvar kvádru s délkou 19 m, šířkou 20 dm a hloubkou 36 cm. Za hodinu vykopou 0,4 m³ zeminy. Kolik času (hodin a minut) potřebují na vyhloubení jámy? - Jáma
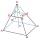 Jáma ve tvaru komolého jehlanu s obdélníkovými podstavami a je hluboká 3,1 m. Délka a šířka jámy je navrchu 3 × 1,5 m, dole 1 m × 0,5 m. Na natření 1 metre čtvereční jámy je třeba 1,4 l zelené barvy. Kolik litrů barvy se na její natření použije, pokud nat
Jáma ve tvaru komolého jehlanu s obdélníkovými podstavami a je hluboká 3,1 m. Délka a šířka jámy je navrchu 3 × 1,5 m, dole 1 m × 0,5 m. Na natření 1 metre čtvereční jámy je třeba 1,4 l zelené barvy. Kolik litrů barvy se na její natření použije, pokud nat - Koule a kužel
 Do koule o poloměru G = 36 cm vepište kužel s největším objemem. Jaký je tento objem a jaké jsou rozměry kužele?
Do koule o poloměru G = 36 cm vepište kužel s největším objemem. Jaký je tento objem a jaké jsou rozměry kužele? - Trojboký hranol
 Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu.
Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu. - Pětiboký jehlan
 Vypočtěte objem pravidelného 5-bokého jehlanu ABCDEV, pokud |AB| = 7,7 cm a roviny ABV, ABC svírají úhel 37 stupňů.
Vypočtěte objem pravidelného 5-bokého jehlanu ABCDEV, pokud |AB| = 7,7 cm a roviny ABV, ABC svírají úhel 37 stupňů. - Řezy kužele
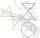 Kužel s poloměrem podstavy 16 cm a výškou 16 cm rozdělíme rovinami rovnoběžnými s podstavou na tři tělesa. Roviny rozdělí výšku kužele na tři stejné části. Určete poměr objemů největšího a nejmenšího vzniklého tělesa.
Kužel s poloměrem podstavy 16 cm a výškou 16 cm rozdělíme rovinami rovnoběžnými s podstavou na tři tělesa. Roviny rozdělí výšku kužele na tři stejné části. Určete poměr objemů největšího a nejmenšího vzniklého tělesa. - Hřiště
 Měřítko mapy je 1: 5000. Hřiště je ve tvaru obdélníku a na mapě má 9 cm a 3 cm. Jakou má výměru v m² ve skutečnosti?
Měřítko mapy je 1: 5000. Hřiště je ve tvaru obdélníku a na mapě má 9 cm a 3 cm. Jakou má výměru v m² ve skutečnosti? - Záhada ze stereometrie
 Dva pravidelné čtyřstěny mají povrchy 72 cm² a 162 cm². V jakém poměru jsou jejich objemy? Zapište jako zlomek a jako řešení zapište i jako desetinné číslo zaokrouhleno na 4 desetinná místa.
Dva pravidelné čtyřstěny mají povrchy 72 cm² a 162 cm². V jakém poměru jsou jejich objemy? Zapište jako zlomek a jako řešení zapište i jako desetinné číslo zaokrouhleno na 4 desetinná místa. - Medaile
 Vypočtěte přibližnou hmotnost zlaté olympijské medaile, má-li průměr 10 cm a tloušťku 6 mm. Hustotu zlata nájdite v tabuľkách alebo na internete.
Vypočtěte přibližnou hmotnost zlaté olympijské medaile, má-li průměr 10 cm a tloušťku 6 mm. Hustotu zlata nájdite v tabuľkách alebo na internete. - Poměr 3
 Tři čísla SUV jsou v poměru 1:2:3. Jejich součet je 66. Nájdi této čísla a zápiš ich sčitovaní.
Tři čísla SUV jsou v poměru 1:2:3. Jejich součet je 66. Nájdi této čísla a zápiš ich sčitovaní. - Letadlo
 Letadlo má v nádržích 59 hl paliva a na každý km letu spotřebuje 3,1 l paliva. Určete funkci, která vyjadřuje závislost množství paliva v nádržích na dráze, kterou letadlo proletělo. Kolik hl paliva má ještě v nádržích ve vzdálenosti 201 km od startu?
Letadlo má v nádržích 59 hl paliva a na každý km letu spotřebuje 3,1 l paliva. Určete funkci, která vyjadřuje závislost množství paliva v nádržích na dráze, kterou letadlo proletělo. Kolik hl paliva má ještě v nádržích ve vzdálenosti 201 km od startu?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
