Příklady na obsah rovinných útvarů - strana 88 z 131
Počet nalezených příkladů: 2608
- Válec + čtyřstěn
 Nádoba tvaru rotačního válce o poloměru podstavy 5 cm je naplněna vodou. O co stoupne hladina vody v nádobě, ponoříme-li do ní pravidelný čtyřstěn o hraně 7cm.
Nádoba tvaru rotačního válce o poloměru podstavy 5 cm je naplněna vodou. O co stoupne hladina vody v nádobě, ponoříme-li do ní pravidelný čtyřstěn o hraně 7cm. - Zaplavila 35023
 Sklep, který má podlahu s plošným obsahem 50 m2, 3 m pod úrovní okolí, zaplavila voda do výšky 80 cm. Za jak dlouho vyčerpá vodu čerpadlo s příkonem 1 kW a účinností 75% (η = 0,75)?
Sklep, který má podlahu s plošným obsahem 50 m2, 3 m pod úrovní okolí, zaplavila voda do výšky 80 cm. Za jak dlouho vyčerpá vodu čerpadlo s příkonem 1 kW a účinností 75% (η = 0,75)? - Vypočítejte 228
 Vypočítejte, kolik hl vody se vejde do padesátimetrového zkoseného bazénu, jestliže nejmenší hloubka je 1,2 m a největší hloubka je 3 m, šířka bazénu je 20 m. Dle vypočítejte, kolik kachlíčků tvaru čtverce o délce strany 15 cm je třeba k vykachlíčkování s
Vypočítejte, kolik hl vody se vejde do padesátimetrového zkoseného bazénu, jestliže nejmenší hloubka je 1,2 m a největší hloubka je 3 m, šířka bazénu je 20 m. Dle vypočítejte, kolik kachlíčků tvaru čtverce o délce strany 15 cm je třeba k vykachlíčkování s - Strana kužele
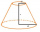 Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°.
Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°. - Povrch a objem
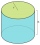 Vypočítejte povrch a objem válce jehož výška je 8 dm a poloměr kružnice podstavy je 2 dm
Vypočítejte povrch a objem válce jehož výška je 8 dm a poloměr kružnice podstavy je 2 dm - Z dřevěného
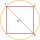 Z dřevěného pravidelného čtyřbokého hranolu (hrana 2,8 cm, výška 7,5 cm ) byl obroušen válec s maximální možnou podstavou. Kolik procent materiálu přišlo na zmar jako odpad? Kolik procent by to bylo, kdyby výška hranolu byla dvojnásobně velká?
Z dřevěného pravidelného čtyřbokého hranolu (hrana 2,8 cm, výška 7,5 cm ) byl obroušen válec s maximální možnou podstavou. Kolik procent materiálu přišlo na zmar jako odpad? Kolik procent by to bylo, kdyby výška hranolu byla dvojnásobně velká? - Správce hradu
 Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří?
Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří? - V krychli
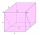 V krychli ABCDA´B´C´D´ je vedena hranou CC´ rovina tak, že rozdělí krychli na dva kolmé hranoly, čtyřboký a trojboký, jejichž objemy jsou v poměru 3 : 2. Určete v jakém poměru je touto rovinou rozdělena hrana AB.
V krychli ABCDA´B´C´D´ je vedena hranou CC´ rovina tak, že rozdělí krychli na dva kolmé hranoly, čtyřboký a trojboký, jejichž objemy jsou v poměru 3 : 2. Určete v jakém poměru je touto rovinou rozdělena hrana AB. - Nádrž
 Nádrž má tvar pravidelného osmibokého hranolu bez horní podstavy. Podstavná hrana má a = 3m, boční hrana b = 6m. Kolik plechu třeba na zhotovení nádrže? Neberte v úvahu ztráty, ani tloušťku plechu.
Nádrž má tvar pravidelného osmibokého hranolu bez horní podstavy. Podstavná hrana má a = 3m, boční hrana b = 6m. Kolik plechu třeba na zhotovení nádrže? Neberte v úvahu ztráty, ani tloušťku plechu. - Hranol
 Objem kolmého čtyřbokého hranolu je 360cm krychlových. Hrany podstavy a výška hranolu jsou v poměru 5:4:2. Určete obsah podstavy a stěn hranolu.
Objem kolmého čtyřbokého hranolu je 360cm krychlových. Hrany podstavy a výška hranolu jsou v poměru 5:4:2. Určete obsah podstavy a stěn hranolu. - Hranol 27
 Hranol s kosočtverečnou podstavou má jednu úhlopříčku podstavy 20 cm a hranu podstavy 26cm. Hrana podstavy je k výšce hranolu v poměru 2:3. Vypočítej objem hranolu.
Hranol s kosočtverečnou podstavou má jednu úhlopříčku podstavy 20 cm a hranu podstavy 26cm. Hrana podstavy je k výšce hranolu v poměru 2:3. Vypočítej objem hranolu. - Předpokládáte 83985
 Stínítko lampy má tvar pláště rotačního kuželu se stranou 32 cm a průměrem podstavy 46 cm. Vypočítejte spotřebu papíru na jeho výrobu pokud předpokládáte, že odpad bude 6%
Stínítko lampy má tvar pláště rotačního kuželu se stranou 32 cm a průměrem podstavy 46 cm. Vypočítejte spotřebu papíru na jeho výrobu pokud předpokládáte, že odpad bude 6% - Vypočítejte 81623
 Sklad má tvar kvádry o rozměrech: délka 50 metrů šířka 600 decimetrů a výška 300 centimetrů. Vypočítejte kolik bude stát malování místnosti bez oken s dveřmi o šířce 150 centimetrů a výšce 200 centimetrů (podlaha se nemaluje), pokud 1 metr ² stojí 1 €.
Sklad má tvar kvádry o rozměrech: délka 50 metrů šířka 600 decimetrů a výška 300 centimetrů. Vypočítejte kolik bude stát malování místnosti bez oken s dveřmi o šířce 150 centimetrů a výšce 200 centimetrů (podlaha se nemaluje), pokud 1 metr ² stojí 1 €. - Terwilliker 75264
 Hromada soli byla uložena ve tvaru kužele. Pan Terwilliker ví, že hromada je 20 stop vysoká a 102 stop v obvodu na základně. Jaká plocha kónické plachty (velký kus materiálu) je potřebná k zakrytí hromady?
Hromada soli byla uložena ve tvaru kužele. Pan Terwilliker ví, že hromada je 20 stop vysoká a 102 stop v obvodu na základně. Jaká plocha kónické plachty (velký kus materiálu) je potřebná k zakrytí hromady? - Čtverečních 71414
 Maťko a Zuzka balí dárky pro otce. Mátko má krabici ve tvaru kvádru o rozměrech 9cm, 3cm, 7cm a Zuzka krabici ve tvaru krychle s délkou hrany 3 cm. Kolik cm čtverečních balicího papíru utratí dohromady, pokud k překrývání potřebují 20% navíc?
Maťko a Zuzka balí dárky pro otce. Mátko má krabici ve tvaru kvádru o rozměrech 9cm, 3cm, 7cm a Zuzka krabici ve tvaru krychle s délkou hrany 3 cm. Kolik cm čtverečních balicího papíru utratí dohromady, pokud k překrývání potřebují 20% navíc? - Majitel
 Majitel nemovitosti chce zateplit svůj dům. Dům má tyto rozměry 12 a12 m je vysoký 15m. Oken má 6 s rozměry 170 a 150 cm. Vchodové dveře mají velikost 250 a 170cm. Kolik metrů čtverečních polystyrenu potřebuje?
Majitel nemovitosti chce zateplit svůj dům. Dům má tyto rozměry 12 a12 m je vysoký 15m. Oken má 6 s rozměry 170 a 150 cm. Vchodové dveře mají velikost 250 a 170cm. Kolik metrů čtverečních polystyrenu potřebuje? - Pravidelného 27601
 Střecha domu má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 100dm. Vypočítejte, kolik m² střešní krytiny je zapotřebí k pokrytí střechy, pokud bereme v úvahu 30% krytiny navíc k překrytí.
Střecha domu má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 100dm. Vypočítejte, kolik m² střešní krytiny je zapotřebí k pokrytí střechy, pokud bereme v úvahu 30% krytiny navíc k překrytí. - Pravidelného 7815
 Obsah pláště pravidelného čtyřbokého jehlanu se rovná dvojnásobku obsahu jeho podstavy. Vypočítej objem jehlanu, pokud délka hrany podstavy je 20 dm.
Obsah pláště pravidelného čtyřbokého jehlanu se rovná dvojnásobku obsahu jeho podstavy. Vypočítej objem jehlanu, pokud délka hrany podstavy je 20 dm. - Komolý jehlan
 Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů.
Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Sklěněné 2
 Sklěněné vánoční ozdoby mají tvar koule s průměrem 8cm. V malé rodinné firmě jich ročně vyrobí 50000 kusů. celý povrch těchto koulí je pokryt třpytkami. Na pokrytí plochy 1m² je potřeba 400 g třpytek. Kolik kilogramu třpytek je potřeba k pokrytí všech vyr
Sklěněné vánoční ozdoby mají tvar koule s průměrem 8cm. V malé rodinné firmě jich ročně vyrobí 50000 kusů. celý povrch těchto koulí je pokryt třpytkami. Na pokrytí plochy 1m² je potřeba 400 g třpytek. Kolik kilogramu třpytek je potřeba k pokrytí všech vyr
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
