Příklady na pravoúhlý trojúhelník - strana 36 z 84
Počet nalezených příkladů: 1676
- Kvádr - úhlopříčka
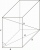 Vypočítej objem kvádru, jehož tělesova úhlopříčka u se rovná 6,1cm a obdélníková postava má rozměry 3,2cm a 2,4cm
Vypočítej objem kvádru, jehož tělesova úhlopříčka u se rovná 6,1cm a obdélníková postava má rozměry 3,2cm a 2,4cm - 4B jehlan - a+h
 Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu ABCDV, má-li jeho podstavná hrana délku a = 10 cm a tělesová výška h = 12 cm.
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu ABCDV, má-li jeho podstavná hrana délku a = 10 cm a tělesová výška h = 12 cm. - Střecha - krytina
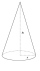 Střecha hradní věže má tvar kužele o průměru podstavy 12 m a výšce 8m. Kolik eur zaplatíme za pokrytí střechy, pokud 1m čtvereční krytiny stojí 3,5 eura?
Střecha hradní věže má tvar kužele o průměru podstavy 12 m a výšce 8m. Kolik eur zaplatíme za pokrytí střechy, pokud 1m čtvereční krytiny stojí 3,5 eura? - Poměr délky úhlopříček
 Délky hran kvádru jsou v poměru 1:2:3. Budou ve stejném poměru i délky jeho stěnových úhlopříček? Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru.
Délky hran kvádru jsou v poměru 1:2:3. Budou ve stejném poměru i délky jeho stěnových úhlopříček? Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru. - Klasický stan
 Stan má tvar trojbokého hranolu. Přední a zadní stěna jsou rovnoramenné trojúhelníky s výškou 18 dm a rameny dlouhými 19,5 dm. Stan je široký 1,5 m a dlouhý 2 m. Kolik m čtverečních látky třeba na zhotovení stanu? Kolik vzduchu se v něm nachází?
Stan má tvar trojbokého hranolu. Přední a zadní stěna jsou rovnoramenné trojúhelníky s výškou 18 dm a rameny dlouhými 19,5 dm. Stan je široký 1,5 m a dlouhý 2 m. Kolik m čtverečních látky třeba na zhotovení stanu? Kolik vzduchu se v něm nachází? - Kvádr
 Rozměry kvádru jsou v poměru 3:1:2. Tělesová úhlopříčka má délku 28cm. Vypočítejte objem kvádru.
Rozměry kvádru jsou v poměru 3:1:2. Tělesová úhlopříčka má délku 28cm. Vypočítejte objem kvádru. - Úhlopříčky kostky
 Kostka má obsah stěny 81 cm². Vypočítej délku její hrany, stěnové a tělesové úhlopříčky.
Kostka má obsah stěny 81 cm². Vypočítej délku její hrany, stěnové a tělesové úhlopříčky. - Vypočítej 93
 Vypočítej povrch pravidelného čtyřbokého jehlanu, jestliže pro jeho objem V a tělesovou výšku v a podstavnou hranu a platí: V = 2,8 m³, v = 2,1 m
Vypočítej povrch pravidelného čtyřbokého jehlanu, jestliže pro jeho objem V a tělesovou výšku v a podstavnou hranu a platí: V = 2,8 m³, v = 2,1 m - Poměr obsahů
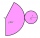 Poměr obsahu podstavy rotačního kužele k jeho plášti je 3:5. Vypočítejte povrch a objem kužele, pokud jeho výška v = 4 cm.
Poměr obsahu podstavy rotačního kužele k jeho plášti je 3:5. Vypočítejte povrch a objem kužele, pokud jeho výška v = 4 cm. - Délky
 Délky hran kvádru jsou v poměru 2:3:6. Jeho tělesová úhlopříčka má délku 14 cm. Vypočtěte objem a povrch kvádru.
Délky hran kvádru jsou v poměru 2:3:6. Jeho tělesová úhlopříčka má délku 14 cm. Vypočtěte objem a povrch kvádru. - Plech na jehlanovou střechu
 Nad pavilonem čtvercového půdorysu se stranou a = 12 m je střecha tvaru jehlanu o výšce 4,5m. Kolik m² plechu je potřeba k zakrytí této střechy?
Nad pavilonem čtvercového půdorysu se stranou a = 12 m je střecha tvaru jehlanu o výšce 4,5m. Kolik m² plechu je potřeba k zakrytí této střechy? - Koule a kužel
 Do koule o poloměru G = 36 cm vepište kužel s největším objemem. Jaký je tento objem a jaké jsou rozměry kužele?
Do koule o poloměru G = 36 cm vepište kužel s největším objemem. Jaký je tento objem a jaké jsou rozměry kužele? - Zavazadla - auto
 Zavazadlový prostor v autě má tvar kvádru s hranami 1,6m x 1,2m x 0,5m (šířka, hloubka, výška). Urči, jakou nejdelší tenkou tyč můžeme položit na dno.
Zavazadlový prostor v autě má tvar kvádru s hranami 1,6m x 1,2m x 0,5m (šířka, hloubka, výška). Urči, jakou nejdelší tenkou tyč můžeme položit na dno. - Stínítko
 Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem
Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem - Do rovnostranného 2
 Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule?
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Povrch pravidelného jehlanu
 Jaký je povrch pravidelného jehlanu se čtvercovou podstavou, pokud každá hrana podstavy měří 40 mm, výška sklonu jehlanu je 44 mm a výška jehlanu je 38 mm?
Jaký je povrch pravidelného jehlanu se čtvercovou podstavou, pokud každá hrana podstavy měří 40 mm, výška sklonu jehlanu je 44 mm a výška jehlanu je 38 mm? - Rotační 15
 Rotační kužel má poloměr podstavy r=226mm, odchylka strany od roviny podstavy je 56°. Vypočtěte výšku kuželu.
Rotační kužel má poloměr podstavy r=226mm, odchylka strany od roviny podstavy je 56°. Vypočtěte výšku kuželu. - Rotace
 Pravoúhlý trojúhelník má strany a = 11 a b = 10. Přepona je c. Pokud se trojúhelník otáčí kolem strany c jako osa, najděte objem a plochu povrchu kuželové plochy vytvořené touto rotací.
Pravoúhlý trojúhelník má strany a = 11 a b = 10. Přepona je c. Pokud se trojúhelník otáčí kolem strany c jako osa, najděte objem a plochu povrchu kuželové plochy vytvořené touto rotací. - Čtyřboký jehlan
 V pravidelném čtyřbokém jehlanu je tělesová výška 38 cm a stěnová výška 42 cm. Vypočítej povrch jehlanu; výsledek zaokrouhli na čtverečné centimetry.
V pravidelném čtyřbokém jehlanu je tělesová výška 38 cm a stěnová výška 42 cm. Vypočítej povrch jehlanu; výsledek zaokrouhli na čtverečné centimetry. - Pokrytí střechy
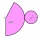 Kolik m² střešní krytiny je potřeba na pokrytí střechy tvaru kužele o průměru 10 m a výšce 4 m? Na překryvy počítej 4 % navíc.
Kolik m² střešní krytiny je potřeba na pokrytí střechy tvaru kužele o průměru 10 m a výšce 4 m? Na překryvy počítej 4 % navíc.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
