Příklady na pravoúhlý trojúhelník - strana 35 z 84
Počet nalezených příkladů: 1676
- Rovnostranné těleso
Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a=2 cm kolem jedné z jeho stran. Vypočítejte objem tohoto rotačního tělesa. - 3B hranol - stan
Kolik m² látky je třeba na zhotovení stanu pravidelného 3-bokého hranolu pokud je třeba počítat s 2% rezervou látky? Rozměry - 2m 1,6m a výška 1,4m - Truhlář
Kvádr s podstavou a rozměry 12 cm a 5 cm a výšce 4 cm. Truhlář tento kvádr rozřezal na dva shodné trojboké hranoly s podstavami ve tvaru pravoúhlého trojúhelníku. Truhlář vytvořeny hranoly natřel barvou. Vypočítejte povrch jednoho z těchto dvou trojbokých - Komolý jehlan
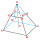Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Roviny bočních stěn
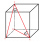Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’ - Rotační telesa
Rotační kužel a rotační válec mají stejný objem 180 cm³ a stejnou výšku v=15cm. Které z těchto dvou těles má větší povrch? - Průměr
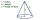Průměr základny pravoúhlého kužele je 16 cm a jeho šikmá výška je 12 cm. A. ) Zjistěte kolmou výšku kužele na 1 desetinné místo. B. ) Najděte objem kužele a přepočítejte ho na 3 významné číslo. Použijte pi = 3,14 - Správce hradu
Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří? - Podstava
Podstavu kolmého hranolu tvoří pravoúhlý trojúhelník, jehož odvěsny mají poměr 3:4. Výška hranolu je o 2cm menší, než větší odvěsna. Určitě objem hranolu, pokud jeho povrch je 468 cm². - Rotační kužel
Objem rotačního kužele je 733 cm³ a strana kužele svírá s rovinou podstavy úhel 75°. Vypočítejte obsah pláště rotačního kužele. - Koule 24
V krychli je naskládáno 9 shodných koulí a to tak, aby co nejvíce vyplnily objem krychle. Jakou část objemu krychle vyplní? - Osový řez
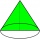Osový řez kužele je rovnoramenný trojúhelník, v němž je poměr průměru kužele a stěny kužele 2:3. Vypočtěte jeho objem, pokud víte, že jeho plocha je 314 cm čtverečních. - Kužel
Vypočtěte objem a plochu kužele, jehož výška je 10 cm a v osovém řezu svírá se stěnou kužele úhel 30 stupňů. - Hranol 4b 2
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa. - Zakrytí hromady soli
Hromada soli byla uložena ve tvaru kužele. Pan Terwilliker ví, že hromada je 20 stop vysoká a 102 stop v obvodu na základně. Jaká plocha kónické plachty (velký kus materiálu) je potřebná k zakrytí hromady? - Vypočítejte 49
Vypočítejte objem V a povrch S pravidelného čtyřbokého jehlanu, jehož hrana podstavy i výška mají stejnou velikost jako hrana krychle o objemu V1=27m3 - Úhel úhlopříčky V pravidelném 4-bokem jehlanu zvíře boční hrana s úhlopříčkou podstavy úhel 55°. Délka boční hrany je 8 m. Vypočtěte povrch a objem jehlanu.
- Stínidlo
Stínidlo ve tvaru kužele má průměr 30 cm a výšku 10 cm. Kolik cm² materiálu budeme potřebovat, počítáme-li 10% na odpad? - Kužel 16
Povrch rotačního kužele je 30 cm2, obsah jeho pláště je 20 cm². Vypočtěte odchylku strany tohoto kužele od roviny podstavy. - Vzduch ve staně
Vypočítejte, kolik litrů vzduchu se vejde do stanu, který má štít tvaru rovnoramenného pravoúhlého trojúhelníku s rameny r dlouhými 3 m, výškou v = 1,5 m a délce d = 5 m.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
