Délky
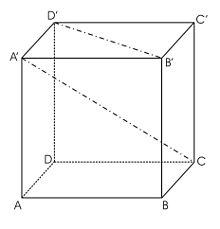
Délky hran kvádru jsou v poměru 2:3:6. Jeho tělesová úhlopříčka má délku 14 cm. Vypočtěte objem a povrch kvádru.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Poměr délky úhlopříček
Délky hran kvádru jsou v poměru 1:2:3. Budou ve stejném poměru i délky jeho stěnových úhlopříček? Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru. - Kvádr 54
Kvádr má rozměry 15, 20 a 40 cm. Vypočtěte jeho objem a povrch, délku tělesové úhlopříčky a délky všech tří stěnových úhlopříček. - Úhlopříčka kvádru
Vypočítejte délku tělesové úhlopříčky kvádru, jehož dvě hrany jsou dlouhé 2 cm a 7 cm, a jeho objem se rovná 49 centimetrů kubických. - Kvádr - poměr
Rozměry kvádru jsou v poměru 4:3:5 , nejkratší hrana kvádru má délku 12 cm. Vypočítej a) délky zbývajících hran, b) povrch kvádru, c) objem kvádru - Objem 30
Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru. - Délky hran
Vypočítejte objem a povrch kvádru, jehož délky hran jsou v poměru 2:3:4 a nejdelší hrana měří 10 cm. - Povrch 33 Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru.
