Angled cyclist turn
The cyclist passes through a curve with a radius of 20 m at 25 km/h. How much angle does it have to bend from the vertical inward to the turn?
Correct answer:
Showing 1 comment:
Matematik
A cyclist has to bend slightly towards the center of the circular track in order to make a safe turn without slipping.
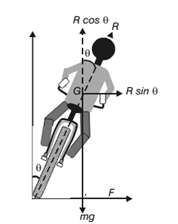
Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components:
(i) the component R sin θ, acting towards the center of the curve providing necessary centripetal force for circular motion and
(ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.
Thus for less bending of the cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger. let h be the elevation of the outer edge of the road above the inner
edge and l be the width of the road then,
Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components:
(i) the component R sin θ, acting towards the center of the curve providing necessary centripetal force for circular motion and
(ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.
Thus for less bending of the cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger. let h be the elevation of the outer edge of the road above the inner
edge and l be the width of the road then,
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert mass units?
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert mass units?
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- geometry
- vector
- algebra
- equation
- expression of a variable from the formula
- planimetrics
- right triangle
- triangle
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Heat energy
 Energy is measured using the unit Joule (J). Temperature is measured using the unit degree Celsius °C). To increase the temperature of 1 liter of water by 1°C, 4200 J of heat energy is required. (a) Kelly wants to increase the temperature of 2 liters of w
Energy is measured using the unit Joule (J). Temperature is measured using the unit degree Celsius °C). To increase the temperature of 1 liter of water by 1°C, 4200 J of heat energy is required. (a) Kelly wants to increase the temperature of 2 liters of w - Resistance 80577
 Three identical resistors connected in series have a total resistance of 9 ohms. What will be their total resistance when connected in parallel
Three identical resistors connected in series have a total resistance of 9 ohms. What will be their total resistance when connected in parallel - Resistivity 80483
 The heating coil of the cooker has a resistance of 70.5 ohms and is made of a wire with a diameter of 0.30 mm and a length of 9.8 m. Determine the resistivity of the material from which it is made.
The heating coil of the cooker has a resistance of 70.5 ohms and is made of a wire with a diameter of 0.30 mm and a length of 9.8 m. Determine the resistivity of the material from which it is made. - Cross-section 71254
 The steel conductors of the long-distance power line have a cross-section of 5 cm². Calculate the resistance of a steel wire with a length of 2 km if the resistivity of the steel is 13 * 10-8 Ω · m.
The steel conductors of the long-distance power line have a cross-section of 5 cm². Calculate the resistance of a steel wire with a length of 2 km if the resistivity of the steel is 13 * 10-8 Ω · m.
- A fan
 A fan with a resistance of 20 Ω is connected to a power supply. The current flowing through the circuit is 2.5 A. What is the voltage of the power supply?
A fan with a resistance of 20 Ω is connected to a power supply. The current flowing through the circuit is 2.5 A. What is the voltage of the power supply? - Resistance 66074
 Determine the current flowing through the car's starter, whose resistance is 60 milliohms at 12V
Determine the current flowing through the car's starter, whose resistance is 60 milliohms at 12V - Resistance 66054
 The handset has a resistance of 4000 ohms. Calculate what voltage is connected to them if the current passes 2.5mA.
The handset has a resistance of 4000 ohms. Calculate what voltage is connected to them if the current passes 2.5mA. - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Voltage - Kirchoff laws
 At a voltage of 2.5V, a current I1= 20mA flows through the resistor. What will the voltage be at the resistor's ends when the current I2= 1,2A passes through it?
At a voltage of 2.5V, a current I1= 20mA flows through the resistor. What will the voltage be at the resistor's ends when the current I2= 1,2A passes through it?
- Cooker spiral
 A current of 4.4 A flows through the spiral of the electric cooker. It is connected to a voltage of 220 V. What is the resistance of the spiral?
A current of 4.4 A flows through the spiral of the electric cooker. It is connected to a voltage of 220 V. What is the resistance of the spiral? - Manganin
 How long must a manganin wire with a diameter of 0.8 mm have a value of 10Ω?
How long must a manganin wire with a diameter of 0.8 mm have a value of 10Ω? - Direction indicator
 When a current of 1.6 A passes through the lamp direction indicator's 7400 mOhm resistance, which voltage is connected to it?
When a current of 1.6 A passes through the lamp direction indicator's 7400 mOhm resistance, which voltage is connected to it? - Circuit voltage
 Calculate the closed-circuit voltage. Calculate the power on the resistors. R1 = 30 ohms, R2 = 10 ohms. I = 0.1A. U =?. The resistors are connected in series, one after the other.
Calculate the closed-circuit voltage. Calculate the power on the resistors. R1 = 30 ohms, R2 = 10 ohms. I = 0.1A. U =?. The resistors are connected in series, one after the other. - Copper winding
 Calculate the current flowing through the copper winding at an operating temperature of 70°C Celsius if the winding diameter is 1.128 mm and the coiled length is 40 m. The winding is connected to 8V.
Calculate the current flowing through the copper winding at an operating temperature of 70°C Celsius if the winding diameter is 1.128 mm and the coiled length is 40 m. The winding is connected to 8V.
- Current in the conductor
 Calculate the current in the conductor (in mA) if it is connected to a 4.5 V voltage source and its resistance is 20 (ohm).
Calculate the current in the conductor (in mA) if it is connected to a 4.5 V voltage source and its resistance is 20 (ohm). - Candles
 Before Christmas, Eva bought two cylindrical candles - red and green. Red was 1 cm longer than green. She lit a red candle on Christmas Day at 5:30 PM, lit a green candle at 7:00 PM, and left them on fire until it burned. At 9:30 PM, both candles were the
Before Christmas, Eva bought two cylindrical candles - red and green. Red was 1 cm longer than green. She lit a red candle on Christmas Day at 5:30 PM, lit a green candle at 7:00 PM, and left them on fire until it burned. At 9:30 PM, both candles were the - Two resistors
 Two resistors, 20 Ω, and 60 Ω, are connected in series, and an external voltage of 400 V is connected to them. What are the electrical voltages on the respective resistors? Please comment!
Two resistors, 20 Ω, and 60 Ω, are connected in series, and an external voltage of 400 V is connected to them. What are the electrical voltages on the respective resistors? Please comment!
