Planimetrics - math word problems - page 162 of 185
Number of problems found: 3685
- Seats on carousel
 There are 12 seats evenly distributed on the children's carousel in the shape of a circle. How long is the arm of the carousel (connecting the center of the carousel to the seat) if the distance between the two seats is 1.5m?
There are 12 seats evenly distributed on the children's carousel in the shape of a circle. How long is the arm of the carousel (connecting the center of the carousel to the seat) if the distance between the two seats is 1.5m? - The rescue helicopter
 The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site?
The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site? - Steps
 Find the height between the two floors if you know that the number of steps between the two floors is 18, the gradient is 30º, and the step length is 28.6 cm. Report the result in centimeters to the nearest centimeter.
Find the height between the two floors if you know that the number of steps between the two floors is 18, the gradient is 30º, and the step length is 28.6 cm. Report the result in centimeters to the nearest centimeter. - A rhombus 4
 A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution. - A construction
 A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an elevation angle of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find the
A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an elevation angle of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find the - Observation 17433
 The aircraft flying just above point A can be seen from observation B, 2,400 meters away from point A, at an altitude of 52°30'. How high does the plane fly?
The aircraft flying just above point A can be seen from observation B, 2,400 meters away from point A, at an altitude of 52°30'. How high does the plane fly? - Components 2565
 The component is a regular decagon with a side of 2 cm. Its material weight of 1 m² of sheet metal is 24 kg. What is the weight of 200 components?
The component is a regular decagon with a side of 2 cm. Its material weight of 1 m² of sheet metal is 24 kg. What is the weight of 200 components? - 30-gon
 The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area.
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - Bridge across the river
 The width of the river is 89 m. For terrain reasons, the bridge deviates from a common perpendicular to both banks by an angle of 12° 30 '. Calculate how many meters the bridge is longer than the river.
The width of the river is 89 m. For terrain reasons, the bridge deviates from a common perpendicular to both banks by an angle of 12° 30 '. Calculate how many meters the bridge is longer than the river. - Elevation angles
 Two endpoints distant 240 m are inclined at an angle of 18°15'. The top of the mountain can be seen at elevation angles of 43° and 51° from its. How high is the mountain?
Two endpoints distant 240 m are inclined at an angle of 18°15'. The top of the mountain can be seen at elevation angles of 43° and 51° from its. How high is the mountain? - Diagonals 5113
 The diagonals in diamond KLMN are 10 cm and 6 cm long. Determine the angle size that the longer diagonal makes with the side of the diamond.
The diagonals in diamond KLMN are 10 cm and 6 cm long. Determine the angle size that the longer diagonal makes with the side of the diamond. - Determine 83081
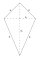 A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid.
A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid. - Triangle SAS
 Calculate the triangle area and perimeter if the two sides are 46 m and 33 m long and angle them clamped is 170 °.
Calculate the triangle area and perimeter if the two sides are 46 m and 33 m long and angle them clamped is 170 °. - Flowerbed
 The flowerbed has the shape of an obtuse isosceles triangle. The arm has a size of 7.6 meters, and an angle opposite the base size is 124°. What is the distance from the base to the opposite vertex?
The flowerbed has the shape of an obtuse isosceles triangle. The arm has a size of 7.6 meters, and an angle opposite the base size is 124°. What is the distance from the base to the opposite vertex? - Steeple
 The church tower is seen from the road at an angle of 52°. When we zoom out to 29 meters away, it can be seen at an angle of 21°. How high is it?
The church tower is seen from the road at an angle of 52°. When we zoom out to 29 meters away, it can be seen at an angle of 21°. How high is it? - Angles of elevation
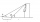 From points A and B on level ground, the angles of elevation of the top of a building are 25° and 37°, respectively. If |AB| = 57m, calculate, to the nearest meter, the distances of the top of the building from A and B if they are both on the same side of
From points A and B on level ground, the angles of elevation of the top of a building are 25° and 37°, respectively. If |AB| = 57m, calculate, to the nearest meter, the distances of the top of the building from A and B if they are both on the same side of - Two boats
 Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface.
Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface. - Sailboat
 The 20 m long sailboat has an 8 m high mast in the middle of the deck. The top of the mast is fixed to the bow and stern with a steel cable. Determine how much cable is needed to secure the mast and what angle the cable will make with the ship's deck.
The 20 m long sailboat has an 8 m high mast in the middle of the deck. The top of the mast is fixed to the bow and stern with a steel cable. Determine how much cable is needed to secure the mast and what angle the cable will make with the ship's deck. - Colored area
 How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - Black diamond run
 Taleah is skiing down a black diamond run. She begins skiing at the top of a ski trail whose elevation is about 8625 feet. The ski run ends toward the base of the mountain at 3800 feet. The horizontal distance between these two points is about 4775 feet.
Taleah is skiing down a black diamond run. She begins skiing at the top of a ski trail whose elevation is about 8625 feet. The ski run ends toward the base of the mountain at 3800 feet. The horizontal distance between these two points is about 4775 feet.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
