Matematická olympiáda - príklady - strana 6 z 11
Počet nájdených príkladov: 206
- Z7–I–4 2018 MO Betka
Betka sa hrala s ozubenými kolesami, ktoré ukladala tak, ako je naznačené na obrázku. Keď potom zatočila jedným okolo, točili sa všetky ostatné. Nakoniec bola spokojná so súkolesím, pričom prvé koleso malo 32 a druhé 24 zubov. Keď sa tretie koleso otočilo - MO Z8–I–5 - 2018
Kráľ dal murárovi Václavovi za úlohu postaviť múr hrubý 25 cm, dlhý 50 m a vysoký 2 m. Ak by Václav pracoval bez prestávky a rovnakým tempom, postavil by múr za 26 hodín. Podľa platných kráľovských nariadení však musí Václav dodržiavať následujúce podmien - MO Z8–I–6 2018
V lichobežníku KLMN má základňa KL veľkosť 40 cm a základňa MN má velkosť 16 cm. Bod P leží na úsečke KL tak, že úsečka NP rozdeľuje lichobežník na dve časti s rovnakými obsahmi. Určte veľkosť úsečky KP. - Z9–I–1 2018 čísla
Nájdite všetky kladné celé čísla x a y, pre ktoré platí: 1/x + 1/y = 1/4 . - Z7-1-3 MO 2018
Dedo pripravil pre svojich šesť vnúčat kôpku lieskových orieškov s tým, nech si ich nejako rozoberú. Prvý prišiel Adam, odpočítal si polovicu, pribral si ešte jeden oriešok a odišiel. Rovnako sa zachoval druhý Bob, tretí Cyril, štvrtý Dano aj piaty Edo. I - Z9-I-4 2018 Hotelier
Hotelier chcel vybaviť jedáleň novými stoličkami. V katalógu si vybral typ stoličky. Až pri zadávaní objednávky sa od výrobcu dozvedel, že v rámci zľavovej akcie ponúkajú každú štvrtú stoličku za polovičnú cenu a že teda oproti plánu môže ušetriť za sedem - Z9 – I – 2 MO 2018
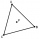V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM.
- Posledná cifra
Aké je posledné číslo 2016-tej mocniny čísla 2017? - Adam mal
Adam mal tri zhodné obdĺžniky. Priložil ich k sebe a dostal obdĺžnik s obvodom 50 cm. Potom ich priložil inak a dostal obdĺžnik s väčším obvodom. Vypočítaj jeho obvod. - Triangulácia 3 body
Z bodu A do B je to 16 km. z bodu C do B je to 20 km z bodu C do D je to 19 km koľko kilometra to je z bodu D do bodu A - C–I–4 MO 2017
Určte najväčšie celé číslo n, pri ktorom možno štvorcovú tabuľku n × n zaplniť prirodzenými číslami od 1 po n² tak, aby v každej jej štvorcovej časti 3 × 3 bola zapísaná aspoň jedna druhá mocnina celého čísla - MAKS bežecká 2017
Mišo a Rišo behali po bežeckej dráhe tam a späť. Rozbehli sa oproti sebe, každý z iného konca dráhy. Obaja stále bežali rovnakou rýchlosťou, každý inou. Prvý raz sa stretli 800 m od jedného konca dráhy, druhý raz na druhom konci dráhy. Akú dĺžku má bežeck - MO Z6-1-3 2017 šachovnica
Veronika má klasickú šachovnicu s 8×8 políčkami. Riadky sú označené ciframi 1 až 8, stĺpce písmenami A až H. Veronika položila na políčko B1 jazdca, s ktorým možno pohybovať iba tak ako v šachu. 1. Je možné premiestniť jazdca štyrmi ťahmi na políčko H1? 2 - Z7-I-5 MO 2017
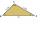Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom - Z7-1-6 MO 2017
Vodník Chaluha nalieval hmlu do rozmanitých rôzne veľkých nádob ktoré si starostlivo zoradil na polici. Pri nalievaní postupoval postupne z jednej strany žiadnu nádobu nepreskakoval. Do každej nádoby sa vojde aspoň deciliter hmly. Keby nalieval hmlu sedem
- Z8-I-6 MO 2017
Priamka predstavuje číselnú os a vyznačené body zodpovedajú číslam a, −a, a + 1, avšak nie nutne v tomto poradí. Zostrojte body, ktoré zodpovedajú číslam 0 a 1. Preberte všetky možnosti. - Z9-I-6 MO 2017
Na priamke predstavujúcej číselnú os uvážte navzájom rôzne body zodpovedajúce číslam a, 2a, 3a + 1 vo všetkých možných poradiach. Pri každej možnosti rozhodnite, či je také usporiadanie možné. Ak áno, uveďte konkrétny príklad, ak nie, zdôvodnite prečo. - Z5–I–6 MO 2017
Na stole ležalo osem kartičiek s číslami 2,3,5,7,11,13,17,19. Fero si vybral tri kartičky. Sčítal na nich napísané čísla a zistil, že ich súčet je o 1 väčší ako súčet čísel na zvyšných kartičkách. Ktoré kartičky mohli zostať na stole? Určte všetky možnost - Z7-I-4 MO 2017
Na stole ležalo šesť kartičiek s ciframi 1, 2, 3, 4, 5, 6. Anežka z týchto kartičiek zložila šesťciferné číslo, ktoré bolo deliteľné šiestimi. Potom postupne odoberala kartičky sprava. Keď odobrala prvú kartičku, zostalo na stole päťciferné číslo deliteľn - Z9-I-5 MO 2017 obdlžník
Vnútri obdlžníka ABCD ležia body M a N. Strana AB je 22 cm a kružnica opísaná trojuholníku AND má polomer 10cm a úsečky MA, MD, MN, NB a NC sú navzájom zhodné. Určite dĺžku strany BC.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
