Příklady na obsah trojúhelníka - strana 30 z 45
Počet nalezených příkladů: 890
- Astronaut
Do jaké výšky musí být chlapec zvednutý nad Zemi, aby mohl vidět jednu pětinu jejího povrchu? - Kůlna
Kůlna tvaru kvádru je kryta střechou tvaru čtyřbokého jehlanu s podstavou o hranách 6 m a 3 m a výškou 2,5 m. Kolik m² (metrů čtverečních) je třeba zakoupit, jestliže na překrytí krytiny a odpad se počítá 40% navíc? - Kruhový bazén
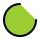Podstava bazénu má tvar kruhu o poloměru r = 10 m kromě kruhového odstavce, který určuje tětiva délky 10 m. Jeho hloubka je h = 2 m. Kolik hektolitrů vody se vejde do bazénu? - Stříška
Pan Peter má nad studní plechovou stříšku tvaru kužele o výšce 101 cm a poloměru 189 cm. Stříška potřebuje natřít antikorozní barvou. Kolik kg barvy musí nakoupit, jestliže výrobce udává spotřebu 1 kg na 4,3 m²? - Střecha
Nad pavilonem se čtvercovým půdorysem se stranou délky a = 12 m je střecha tvaru pláště jehlanu s výškou v = 4,5 m. Vypočítejte, kolik m² plechu třeba k zakrytí této střechy, jestliže na spoje a odpad třeba počítat 5,5% plechu. - Dětský bazénik
Dno dětského bazénku je pravidelný šestiúhelník se stranou a = 60 cm. Vzdálenost protilehlých stran je 104 cm, výška bazénku je 45 cm. A) Kolik litrů vody se vejde do bazénku? B) Bazének je vyroben ze dvojité vrstvy plastové fólie. Minimálně kolik m² fóli - Skleník 2
Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr - Plech 3
Kolik m² pozinkovaného plechu se spotřebuje na pokrytí střechy věže, která má tvat čtyřbokohého jehlanu, jehož podstava hrany má délku 6 m. Výška věže je 9 m. Při pokrývání se počítá s 5 % odpadem plechu? - Součet velikostí hran
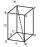Vypočtěte povrch kvádru, je-li dán součet velikostí jeho hran a+b+c=19 cm a velikost tělesové úhlopříčky u=13 cm. - Čtyřboký jehlan
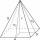Jaký je povrch pravidelného čtyřbokého jehlanu, když je podstavná hrana a=16 a výška v=19? - Cena střechy
Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg. - Kosý hranol
Jaký objem má čtyřboký kosý hranol s podstavnými hranami o délce a=1 m, b=1,1 m, c=1,2 m, d=0,7 m, jestliže boční hrana o délce h=3,9 m má odchylku od podstavy 20°35´ a hrany a, b svírají úhel 50,5°. - V pravidelném 2
V pravidelném čtyřbokem jehlanu je výška 6,5 cm a úhel mezi podstavou a boční stěnou je 42°. Vypočítej povrch a objem tělesa. Výpočty zaokrouhlit na 1 desetinné místo. - Krabička
Kartonová krabička tvaru čtyřbokého hranolu s kosočtvercovou podstavou. Kosočtverec má stranu 5 cm a jednu uhlopříčku 8 cm výška krabičky je 12 cm. Krabička bude nahoře otevřená. Kolik cm² kartonu budeme potřebovat na překrytí a na spoje, které jsou 5% ka - Podstava RR licho
Podstavou hranolu je rovnoramenný lichoběžník ABCD se základnami AB = 12 cm, CD = 9 cm. Úhel při vrcholu B je 48° 10'. Určete objem a porch hranolů, je-li jeho výška 35 cm. - Cena plechu na jehlan
Obvod štvobokého ihlava je 48 m a jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1 m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby. - Stanové plátno
Stan tvaru jehlanu má podstavu čtverce o velikosti strany 2,2 m a výšku 1,8 m. Kolik metrů čtverečních stanového plátna je třeba na jeho zhotovení počítáme-li pět procent navíc na založení? - Krabice
Vypočítaj spotřebu papíru na krabici tvaru čtyřbokého hranolu s kosočtvercovou podstavou, podstavná hrana a=6 cm, sousedící hrany svírá úhel alfa=60°. výška krabice je 10 cm. Kolik m² papíru spotřebujeme na 100 takových krabic? - Střecha domu
Střecha domu má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 13 m. Kolik m² je třeba na její pokrytí, jestliže sklon střechy 31° a na spoje a odpad počítáme 11% plechu navíc? - Pravidelného 4BJ Objem pravidelného čtyřbokého jehlanu je 72 cm³. Jeho výška se rovná délce podstavné hrany. Vypočítej délku podstavné a povrch jehlanu.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
