Čtyřboký jehlan
Jaký je povrch pravidelného čtyřbokého jehlanu, když je podstavná hrana a=16 a výška v=19?
Správná odpověď:
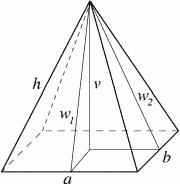
Zobrazuji 2 komentáře:
Žák
Úplně zbytečně se počítá "u" a "h", stačí "w1" vypočítat jako přeponu pravoúhlého trojúhelníku s odvěsnami "v" a "a/2"
6 let 2 Likes
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
aritmetikastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Čtyřbokého jehlanu
Jaký je objem pravidelného čtyřbokého jehlanu, jestliže jeho povrch je 576 cm² a podstavná hrana 16 cm? - Vypočítej 77
Vypočítej objem pravidelného čtyřbokého jehlanu, jehož podstavná hrana měří 6 cm a výška 10 cm - 4B jehlan - a+h
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu ABCDV, má-li jeho podstavná hrana délku a = 10 cm a tělesová výška h = 12 cm. - Pravidelného 83254
Jaký je objem pravidelného čtyřbokého jehlanu, pokud jeho podstavná hrana a = √18 cm a boční hrana b = 5 cm? - Tělesova výška
Vypočítejte tělesovou výšku v pravidelného čtyřbokého jehlanu o objemu V = 163,3cm3, jehož podstavná hrana má velikost a=0,7dm. - 216 povrch i objem
Vypočítej povrch a objem pravidelného čtyřbokého jehlanu: a = 6 cm a tělesová výška je 12 cm. - Slunečník
Slunečník má tvar pláště šestibokého pravidelného jehlanu, jehož podstavná hrana a=6dm a výška v=25cm. Kolik látky je třeba na zhotovení slunečníku, počítáme-li na spoje a odpad 10%.
