Štvorboký ihlan
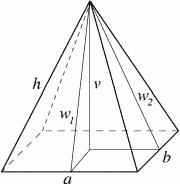
Aký je povrch pravidelného štvorbokého ihlanu, keď je podstavná hrana a=21 a výška v=13?
Vaša odpoveď:
Vaša odpoveď:
Zobrazujem 2 komentáre:
Žiak
na určenie povrchu predsa nepotrebujem stranu h, a načo sa počíta u ? nie je ani označená na obrázku
Dr Math
mate pravdu, zbytocne sme pocitali dlzku bocnej hrany. A z hrany sme pocitali vysku bocneho trojuholnika. Ale ta sa da priamo - z vysky v a dlzky a/2 (w1 je tam je prepona)
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikastereometriaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Objem ihlana
Vypočítaj objem pravidelného štvorbokého ihlanu, ktorého podstavná hrana meria 6 cm a výška 10 cm - Výška ihlanu
Vypočítajte telesovú výšku v pravidelného štvorbokého ihlanu s objemom V = 163,3 cm3, ktorého podstavná hrana má veľkosť a = 0,7 dm. - Vypočítajte 50
Vypočítajte objem a povrch pravidelného štvorbokého ihlana ABCDV, ak jeho podstavná hrana má dĺžku a = 10 cm a telesová výška h = 12 cm. - Ihlan 4b
Vypočítaj objem a povrch pravidelného štvorbokého ihlanu, ak hrana podstavy je 45 cm dlhá a výška ihlanu je 7 cm. - Ihlan 4 boký
Vypočítajte objem a povrch pravidelného štvorbokého ihlanu, ak hrana podstavy je 4 cm dlhá a výška ihlanu je 7 cm. - Plášť hexa-ihlanu
Určte obsah plášťa pravidelného šesťbokého ihlanu, viete ak že jeho podstavná hrana má dĺžku 5 cm a výška tohto ihlanu je 10 cm. - Bočná hrana
Aký je objem pravidelného štvorbokého ihlana, ak jeho podstavná hrana a = √18 cm a bočná hrana b = 5 cm?
