Příklady na obsah úhel - strana 10 z 14
Počet nalezených příkladů: 266
- Šestiúhelník nepravidelný
 Na obrázku je čtverec ABCD, čtverec EF GD a obdélník HIJD. Body J a G leží na straně CD, přičemž platí |DJ| < |DG|, a body H a E leží na straně DA, přičemž platí |DH| < |DE|. Dále víme, že |DJ| = |GC|. Šestiúhelník ABCGFE má obvod 96 cm, šestiúhelní
Na obrázku je čtverec ABCD, čtverec EF GD a obdélník HIJD. Body J a G leží na straně CD, přičemž platí |DJ| < |DG|, a body H a E leží na straně DA, přičemž platí |DH| < |DE|. Dále víme, že |DJ| = |GC|. Šestiúhelník ABCGFE má obvod 96 cm, šestiúhelní - Lichoběžník - úhlopříčky
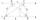 Lichoběžník má délku úhlopříčky AC přeseknutu úhlopříčkou BD v poměru 2:1. Trojúhelník vytvořen body A, průnikem úhlopříček (S) a bodem D má obsah 164 cm². (Tomuto trojúhelníku také patří strana úhlopříčky AC a je 2x větší než její druhá část.) Jaký je ob
Lichoběžník má délku úhlopříčky AC přeseknutu úhlopříčkou BD v poměru 2:1. Trojúhelník vytvořen body A, průnikem úhlopříček (S) a bodem D má obsah 164 cm². (Tomuto trojúhelníku také patří strana úhlopříčky AC a je 2x větší než její druhá část.) Jaký je ob - Z6-I-6 MO 2018
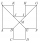 Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct
Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct - Pravoúhlý lichoběžník
 Uveden je pravoúhlý lichoběžník s mírou ostrého úhlu 50°. Délka jeho podstavců je 4 a 6 jednotek. Objem pevné látky získaný rotací daného lichoběžníku kolem delší základny je:
Uveden je pravoúhlý lichoběžník s mírou ostrého úhlu 50°. Délka jeho podstavců je 4 a 6 jednotek. Objem pevné látky získaný rotací daného lichoběžníku kolem delší základny je: - Tvrdé dřevo
 Tvrdé dřevo pro sloup je ve tvaru komolého jehlanu, pravidelné heptagonálnej (hepta = 7) pyramidy. Dolní hrana základny je 18 cm a horní základna 14 cm. Výška je 30 cm. Zjistěte jeho hmotnost v kg, pokud je hustota dřeva 10 gramů / cm³.
Tvrdé dřevo pro sloup je ve tvaru komolého jehlanu, pravidelné heptagonálnej (hepta = 7) pyramidy. Dolní hrana základny je 18 cm a horní základna 14 cm. Výška je 30 cm. Zjistěte jeho hmotnost v kg, pokud je hustota dřeva 10 gramů / cm³. - Koule ve kuželi
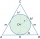 Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t - Komolý jehlan
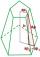 Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm.
Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm. - 4-boký jehlan v2
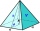 Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů.
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů. - Vrchol 9
 Vrchol věže má tvar pravidelného šestibokého jehlanu. Podstavná hrana má délku 1,2 m, výška jehlanu je 1,6 m. Kolik metrů čtverečných plechu je potřeba na pokrytí vrcholu věže, je-li na spoje, překrytí a odpad zapotřebí 15% plechu navíc?
Vrchol věže má tvar pravidelného šestibokého jehlanu. Podstavná hrana má délku 1,2 m, výška jehlanu je 1,6 m. Kolik metrů čtverečných plechu je potřeba na pokrytí vrcholu věže, je-li na spoje, překrytí a odpad zapotřebí 15% plechu navíc? - Krabice s džusem
 Krabice s džusem má tvar kvádru. Vnitřní rozměry jejich stran jsou 15 cm, 20 cm, a 32 cm. Jestliže je krabice postavena na nejmenší podstavě, dosahuje hladina džusu 4 cm pod horní podstavu. Kolik vnitřního objemu krabice vyplňuje džus? Kolik cm pod horní
Krabice s džusem má tvar kvádru. Vnitřní rozměry jejich stran jsou 15 cm, 20 cm, a 32 cm. Jestliže je krabice postavena na nejmenší podstavě, dosahuje hladina džusu 4 cm pod horní podstavu. Kolik vnitřního objemu krabice vyplňuje džus? Kolik cm pod horní - Kužel
 Vypočítej objem a povrch kužele, pokud průměr podstavy je d = 14 cm a strana kužele svírá s rovinou podstavy úhel 34°24'.
Vypočítej objem a povrch kužele, pokud průměr podstavy je d = 14 cm a strana kužele svírá s rovinou podstavy úhel 34°24'. - Kužel S2V
 Plášť kužele rozvinutý do roviny má tvar kruhové výseče se středovým úhlem 126° a obsahem 415 cm². Vypočítejte objem tohoto kužele.
Plášť kužele rozvinutý do roviny má tvar kruhové výseče se středovým úhlem 126° a obsahem 415 cm². Vypočítejte objem tohoto kužele. - Věž
 Kolik m² měděného plechu třeba na výměnu střechy věže kuželovitého tvaru, jejíž průměr je 10 m a úhel při vrcholu v osovém řezu je 143°?
Kolik m² měděného plechu třeba na výměnu střechy věže kuželovitého tvaru, jejíž průměr je 10 m a úhel při vrcholu v osovém řezu je 143°? - Jehlan
 Urči povrch pravidelného čtyřbokého jehlanu, když je dán jeho objem V = 120 a úhel boční stěny s rovinou podstavy je α = 42° 30'.
Urči povrch pravidelného čtyřbokého jehlanu, když je dán jeho objem V = 120 a úhel boční stěny s rovinou podstavy je α = 42° 30'. - Střecha
 Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem.
Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem. - Střecha domu
 Střecha domu má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 13 m. Kolik m² je třeba na její pokrytí, jestliže sklon střechy 31° a na spoje a odpad počítáme 11% plechu navíc?
Střecha domu má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 13 m. Kolik m² je třeba na její pokrytí, jestliže sklon střechy 31° a na spoje a odpad počítáme 11% plechu navíc? - Kruhový bazén
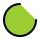 Podstava bazénu má tvar kruhu o poloměru r = 10m kromě kruhového odstavce, který určuje tětiva délky 10m. Jeho hloubka je h = 2m. Kolik hektolitrů vody se vejde do bazénu?
Podstava bazénu má tvar kruhu o poloměru r = 10m kromě kruhového odstavce, který určuje tětiva délky 10m. Jeho hloubka je h = 2m. Kolik hektolitrů vody se vejde do bazénu? - Čtyřboký jehlan
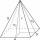 Jaký je povrch pravidelného čtyřbokého jehlanu, když je podstavná hrana a=16 a výška v=19?
Jaký je povrch pravidelného čtyřbokého jehlanu, když je podstavná hrana a=16 a výška v=19? - Cena střechy
 Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg.
Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg. - Dětský bazénik
 Dno dětského bazénku je pravidelný šestiúhelník se stranou a = 60cm. Vzdálenost protilehlých stran je 104cm, výška bazénku je 45cm. A) Kolik litrů vody se vejde do bazénku? B) Bazének je vyroben z dvojité vrstvy plastové fólie. Minimálně kolik m² fólie tř
Dno dětského bazénku je pravidelný šestiúhelník se stranou a = 60cm. Vzdálenost protilehlých stran je 104cm, výška bazénku je 45cm. A) Kolik litrů vody se vejde do bazénku? B) Bazének je vyroben z dvojité vrstvy plastové fólie. Minimálně kolik m² fólie tř
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
