Komolý jehlan
Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm.
Vaše odpověď:
Vaše odpověď:
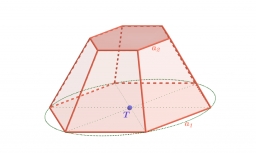
Zobrazuji 1 komentář:
Žák
Q:máte tam chybu u X=... (30-12) na druhou má být ještě děleno 2
A: je to ok. osovy rez cez hranu je pravouhly lichobeznik se stranami a1,a2 vyskou h a bocni stranou s. z toho pak pytagorovou vetou vypocteme vysku telesa. delit dvema nema smysl.
A: je to ok. osovy rez cez hranu je pravouhly lichobeznik se stranami a1,a2 vyskou h a bocni stranou s. z toho pak pytagorovou vetou vypocteme vysku telesa. delit dvema nema smysl.
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Chcete proměnit jednotku délky?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraaritmetikastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Počet sázení pro záhon
Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10 m, horní podstavy je 9 m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysázení 1 m čtverečního je třeba 90? - Květinový záhon
Květinový záhon má tvar komolého jehlanu, přičemž hrana dolní podstavy a = 10 m, horní podstavy b = 9 m a odchylka počne hrany od podstavy je alfa = 45°. Jaký objem zemniny je potřebný navýšit na tento záhon? Kolik sazenic je možné vysadit, pokud 1 m² = 1 - Vypočtěte 6
Vypočtěte povrch a objem pravidelného čtyřbokého jehlanu, je-li hrana dolní podstavy 18 cm a hrana horní podstavy 15 cm. Stěnová výška je 9 cm. - Komolý jehlan
Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Čtyřboký komolý jehlan
Vypočítejte povrch a objem pravidelného čtyřbokého komolého jehlanu, jsou-li hrany podstavy 87 cm a 64 cm a stěnová výška je 49 cm. - Trojboký jehlan
Vypočítejte objem a obsah pravidelného trojbokého jehlanu pokud výška jehlanu je 12 centimetrů, jehož hrana podstavy má 4 centimetry a výška boční stěny 12 cm. - Komolý jehlan 4
Betonový podstavec tvaru pravidelného čtyřbokého komolého jehlanu má výšku 12 cm, hrany podstavy mají délky 2,4 a 1,6 dm. Vypočítej povrch podstavce.
