Příklady na obsah úhel - strana 12 z 14
Počet nalezených příkladů: 266
- 4-boký jehlan v1
 Vypočítej objem a povrch pravidelného 4bokého jehlanu, jehož podstavna hrana je 4 cm. Odchylka bočni steny od roviny je 60 stupňů.
Vypočítej objem a povrch pravidelného 4bokého jehlanu, jehož podstavna hrana je 4 cm. Odchylka bočni steny od roviny je 60 stupňů. - Komolý jehlan
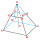 Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů.
Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Rotační kužel
 Objem rotačního kužele je 733 cm³ a strana kužele svírá s rovinou podstavy úhel 75°. Vypočítejte obsah pláště rotačního kužele.
Objem rotačního kužele je 733 cm³ a strana kužele svírá s rovinou podstavy úhel 75°. Vypočítejte obsah pláště rotačního kužele. - Věž
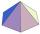 Vrchol věže je pravidelný šestiboký jehlan o podstavné hraně 12 metrů a výšce 7 metrů. Kolik m² plechu je třeba na pokrytí vrcholu věže, počítáme-li na odpad 11%?
Vrchol věže je pravidelný šestiboký jehlan o podstavné hraně 12 metrů a výšce 7 metrů. Kolik m² plechu je třeba na pokrytí vrcholu věže, počítáme-li na odpad 11%? - Strana kužele
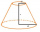 Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°.
Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°. - Nádrž
 Nádrž má tvar pravidelného osmibokého hranolu bez horní podstavy. Podstavná hrana má a = 3m, boční hrana b = 6m. Kolik plechu třeba na zhotovení nádrže? Neberte v úvahu ztráty, ani tloušťku plechu.
Nádrž má tvar pravidelného osmibokého hranolu bez horní podstavy. Podstavná hrana má a = 3m, boční hrana b = 6m. Kolik plechu třeba na zhotovení nádrže? Neberte v úvahu ztráty, ani tloušťku plechu. - Hranol 4b 2
 Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa.
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa. - Vypočítejte 4BH
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Kulový
 Kulový výsek, jehož osový řez má ve středu koule úhel o velikosti α = 120°, je částí koule o poloměru r = 10 cm. Vypočtěte povrch výseku.
Kulový výsek, jehož osový řez má ve středu koule úhel o velikosti α = 120°, je částí koule o poloměru r = 10 cm. Vypočtěte povrch výseku. - Stínítko na lampe
 Stínidlo na lampu na tvář seříznutého kužele o výšce 20 cm. Horní průměr stínítka je 13 cm, dolní 36 cm a strana svírá s dolním průměrem úhel 60 stupňů. Nejméně kolik látky je potřeba k výrobě tohoto stínítka?
Stínidlo na lampu na tvář seříznutého kužele o výšce 20 cm. Horní průměr stínítka je 13 cm, dolní 36 cm a strana svírá s dolním průměrem úhel 60 stupňů. Nejméně kolik látky je potřeba k výrobě tohoto stínítka? - Kužel 16
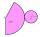 Povrch rotačního kužele je 30 cm2, obsah jeho pláště je 20 cm². Vypočtěte odchylku strany tohoto kužele od roviny podstavy.
Povrch rotačního kužele je 30 cm2, obsah jeho pláště je 20 cm². Vypočtěte odchylku strany tohoto kužele od roviny podstavy. - Zemekoule
 Kolik procent zemského povrchu leží v pásmu tropickém, mírném, arktickém? Hranici mezi pásmy tvoří rovnoběžky 23°27' a 66°33'.
Kolik procent zemského povrchu leží v pásmu tropickém, mírném, arktickém? Hranici mezi pásmy tvoří rovnoběžky 23°27' a 66°33'. - Desaťuholník - hranol
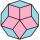 Pravidelný desaťuholník se stranou a = 2 cm je podstavou kolmého hranolu, jehož boční stěny jsou čtverce. Určete objem hranolu v cm³ s přesností na dvě desetinná místa.
Pravidelný desaťuholník se stranou a = 2 cm je podstavou kolmého hranolu, jehož boční stěny jsou čtverce. Určete objem hranolu v cm³ s přesností na dvě desetinná místa. - Základna pyramidy
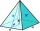 Všechny boční hrany čtyřboké pyramidy ABCDV jsou stejně dlouhé a její základna je obdélník. Určete jeho objem, pokud znáte odchylky rovin sousedních bočních stěn a roviny základny a výšku h pyramidy.
Všechny boční hrany čtyřboké pyramidy ABCDV jsou stejně dlouhé a její základna je obdélník. Určete jeho objem, pokud znáte odchylky rovin sousedních bočních stěn a roviny základny a výšku h pyramidy. - Odchýlka roviny podstavy
 Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°.
Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°. - Kužel
 Obsah pláště kužele je 4 cm², obsah podstavy kužele je 2 cm². Určete v stupních úhel (odchylku) strany kužele a roviny podstavy kužele. (Strana kužele je úsečka spojující vrchol kužele s libovolným bodem kružnice podstavy. Všechny strany kužele tvoří pláš
Obsah pláště kužele je 4 cm², obsah podstavy kužele je 2 cm². Určete v stupních úhel (odchylku) strany kužele a roviny podstavy kužele. (Strana kužele je úsečka spojující vrchol kužele s libovolným bodem kružnice podstavy. Všechny strany kužele tvoří pláš - 6b šestiboký jehlan
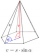 Pravidelný šestiboký jehlan má rozměry: délka hrany podstavy a=1,8dm, výška jehlanu v=2,4dm. Vypočtěte povrch a objem jehlanu.
Pravidelný šestiboký jehlan má rozměry: délka hrany podstavy a=1,8dm, výška jehlanu v=2,4dm. Vypočtěte povrch a objem jehlanu. - Šestiúhelník - jehlan
 Podstavou pravidelného jehlanu je šestiúhelník, kterému je možno opsat kružnici s poloměrem 1m. Vypočitej objem jehlanu vysokého 2,5m.
Podstavou pravidelného jehlanu je šestiúhelník, kterému je možno opsat kružnici s poloměrem 1m. Vypočitej objem jehlanu vysokého 2,5m. - Šestiúhelníkový hranol
 Podstavou hranolu je pravidelný šestiúhelník, který je složen ze šesti trojúhelníků se stranou a = 12 cm a výškou va = 10,4 cm. Výška hranolu je 5 cm. Vypočítejte objem a povrch hranolu!
Podstavou hranolu je pravidelný šestiúhelník, který je složen ze šesti trojúhelníků se stranou a = 12 cm a výškou va = 10,4 cm. Výška hranolu je 5 cm. Vypočítejte objem a povrch hranolu! - Obsah podstavy
 Tyč má tvar pravidelného šestibokého hranolu s objemem 32,4 decimetrech kubického. Jaký je obsah podstavy, pokud je dlouhá 350 centimetrů? Zaokrouhlí na jednotky.
Tyč má tvar pravidelného šestibokého hranolu s objemem 32,4 decimetrech kubického. Jaký je obsah podstavy, pokud je dlouhá 350 centimetrů? Zaokrouhlí na jednotky.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
