Příklady na obsah rovinných útvarů - strana 84 z 126
Počet nalezených příkladů: 2515
- 4-boký jehlan v1
Vypočítej objem a povrch pravidelného 4bokého jehlanu, jehož podstavna hrana je 4 cm. Odchylka bočni steny od roviny je 60 stupňů. - Kvádr
Kvádr má povrch 1819 cm², délky jeho hran jsou v poměru 5:1:4. Vypočítej objem kvádru. - Sklep 3
Nobostavba rodinného domku má být podsklepena. Dno, stěny i strop sklepu mají být potaženy asfaltovou izolační vrstvou. Půdorys rodinného domku má rozměry 10m a 12m. Výška sklepu včetně tloušťky dna a stropu je 3m. 1m čtvereční izolační vrstvy stojí 320 K - Věž
Vrchol věže je pravidelný šestiboký jehlan o podstavné hraně 9,9 metrů a výšce 8,4 metrů. Kolik m² plechu je třeba na pokrytí vrcholu věže, počítáme-li na odpad 5%? - Plášť = 2 x podstava
Pravidelný čtyřboký hranol má objem 864cm³ a obsah jeho pláště je dvojnásobkem obsahu jeho podstavy. Určete velikost jeho tělesové úhlopříčky. - Vydláždění 83106
Hradní nádvoří o rozloze 100 m² je vydlážděno dubovými kostkami o hraně 8 cm. Na vydláždění m² bylo použito přibližně 164 kostek. 1 dm³ dubového dřeva má hmotnost 0,8kg. Vypočítej hmotnost všech kostek, které byly použity k vydláždění nádvoří. - Zaplavila 35023
Sklep, který má podlahu s plošným obsahem 50 m2, 3 m pod úrovní okolí, zaplavila voda do výšky 80 cm. Za jak dlouho vyčerpá vodu čerpadlo s příkonem 1 kW a účinností 75% (η = 0,75)?
- Vodojem 4
Vodojem veřejného vodovodu má vnitřek tvaru krychle. Hrana této krychle má délku 5 m. a) Kolik vody je ve vodojemu, když je zcela naplněn? (Vyjádřete tento objem v m³ a v hektolitrech. ) b) Jak vysoko sahá voda ve vodojemu, když z něho bylo vypuštěno urči - Z dřevěného
Z dřevěného pravidelného čtyřbokého hranolu (hrana 2,8 cm, výška 7,5 cm ) byl obroušen válec s maximální možnou podstavou. Kolik procent materiálu přišlo na zmar jako odpad? Kolik procent by to bylo, kdyby výška hranolu byla dvojnásobně velká? - Těžítko 3
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Obvod 34
Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm². - Vyřízne kvádr
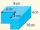Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199 cm³. Vypočítejte hodnotu x. - Astronaut
Jaké procento zemského povrchu vidí astronaut z výšky h = 350 km. Vezměte Zemi jako kouli s poloměrem R = 6370 km - Nádoba 13
Nádoba ve tvaru válce má obsah podstavy 300cm na druhou a výšku 10 cm. Je naplněna z 90% vodou. Do vody vkládáme postupně kovové kuličky, každou o objemu 20 cm na třetí. Po vložení kolikáté kuličky poprvé přeteče voda přes okraj nádoby? - Kruhový 14
Kruhový otvor kontejneru pro vhazování skleněného odpadu má průměr 18cm . Projde tímto otvorem čtyřlitrová sklenice? Jsou li ve sklenici 4litry vody, sahá do výše 20cm
- Magnetického 46021
Vypočítejte energii magnetického pole válcové cívky, která má 400 závitů, délku 0,4 m a poloměr 20 mm. Cévkou prochází proud 3A. (µo = 4π 10-7 H. M-1) - Povrch a objem
Vypočítejte povrch a objem válce jehož výška je 8 dm a poloměr kružnice podstavy je 2 dm - Jáma - jehlanova
Jáma má tvar pravidelného seříznutého 4-bokého jehlanu, jejichž podstavné hrany mají velikosti 14m, 10m a hloubka je 6m. Vypočítejte, kolik m³ zeminy bylo při vyhloubení této jámy vyvezeno. - Rozměry bazénu
Bazén tvaru kvadru o rozměrech dna 7m * 4m a výšce 1,2m je třeba natřít barvou. Kolik bude stát nátěr, když 1 kg barvy, který stačí na 6 m² nátěru, stojí 3 eur. Za nátěr 1 m² si natěrač účtuje 1 eur. - Trubka
Vypočítejte hmotnost plastové trubky s průměrem d = 40 mm a délce 330 cm, pokud tloušťka stěny je 8 mm a hustota plastu je 1360 kg/m³.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
Viz také více informacií na Wikipedii.
