Plášť = 2 x podstava

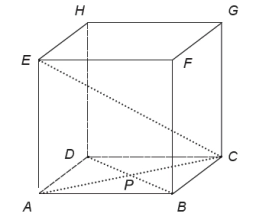
Pravidelný čtyřboký hranol má objem 864 cm³ a obsah jeho pláště je dvojnásobkem obsahu jeho podstavy. Určete velikost jeho tělesové úhlopříčky.

Vaše odpověď:

Pomozte nám příklad zlepšit. Pokud jste našli chybu, dejte nám vědět. Děkujeme!

Tipy na související online kalkulačky

Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

algebra

úpravy výrazů

aritmetika

odmocnina

stereometrie

kvádr
tělesová úhlopříčka
povrch tělesa
hranol

planimetrie

Pythagorova věta
pravoúhlý trojúhelník
obsah

Jednotky fyzikálních veličin

objem
plocha

Úroveň náročnosti úkolu

8. ročník
9. ročník

Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1 video2

Související a podobné příklady:

Čtyřboký hranol
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesové úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru.
Pravidelný 3
Pravidelný čtyřboký hranol má obsah podstavy 25 cm² a povrch 210 cm². Určete objem.
Pravidelný čtyřboký hranol
Pravidelný čtyřboký hranol má hranu podstavy a=7,1 cm a boční hranu =18,2 cm dlouhou. Vypočítejte jeho objem a povrch.
Máme pravidelný
Máme pravidelný čtyřboký jehlan s podstavnou hranou a=10 cm a výškou v=7 cm. Vypočtěte 1/obsah podstavy 2/obsah pláště 3/povrch jehlanu 4/objem jehlanu
Úhlopříčky kvádru
Vypočítej objem kvádru, pokud a=3 cm, velikost tělesové úhlopříčky je 10 cm a velikost úhlopříčky podstavy je 5 cm
Čtyřboký jehlan 9
Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště.
Povrch jehlanu
Obsah pláště pravidelného čtyřbokého jehlanu se rovná dvojnásobku obsahu jeho podstavy. Vypočítej povrch jehlanu, pokud délka hrany podstavy je 20 dm.