Šestiboký hranol 2
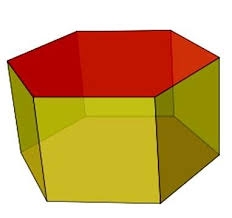
Vypočítej objem pravidelného šestibokého hranolu jehož tělesové úhlopříčky jsou 24cm a 25cm.
Správná odpověď:
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- rovnice
- vyjádření neznámé ze vzorce
- stereometrie
- tělesová úhlopříčka
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- mnohoúhelník
- obsah
- trojúhelník
- úhlopříčka
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Vypočítej 39
Vypočítej objem (V) a povrch (S) pravidelného čtyřbokého hranolu, jehož výška je 28,6 cm a odchylka tělesové úhlopříčky od roviny podlahy je 50°. - Pravidelného 6424
Vypočítej objem a povrch pravidelného šestibokého hranolu, jehož hrana podstavy má délku 5 cm a jeho výška je 20 cm - Tělesová úhlopříčka
Vypočítejte délku tělesové úhlopříčky kvádru, jehož rozměry jsou a=5cm, b=6cm, c=10cm. - Šestiboký hranol
Vypočtěte povrch pravidelného šestibokého hranolu, jehož podstavná hrana a = 12cm a boční hrana b = 3 dm.
- Vypočítejte 4091
Vypočítejte délku tělesové úhlopříčky kvádru, jehož dvě hrany jsou dlouhé 2 cm a 7 cm, a jeho objem se rovná 49 centimetrů kubických. - Vypočítejte 32001
Vypočítejte objem nádoby ve tvaru šestibokého hranolu o výšce 1,4 m, jehož obsah podstavy je 8300 cm². - Hexa hranol Vypočítejte objem a povrch pravidelného šestibokého hranolu s hranou podstavy a = 6cm s příslušnou výškou v1 = 5,2cm a výškou hranolu h = 1dm.
