Základní operace a pojmy - slovní úlohy a příklady - strana 225 z 302
Počet nalezených příkladů: 6029
- Televizní 4
Televizní stanice o svém vysílacím schématu tvrdí, že reklama zabírá 76 minut vysílání během celého dne a vysílá se v náhodných intervalech. a) jaká je pravděpodobnost, že pokud přepnete televizor na tuto stanici, bude vysílat reklamu? b) druhá televizní - Jednotlivých 82716
Na přípravu 14 kg sýra se 45% sušiny smíchali 3 druhy sýrových směsí. První bylo 5 kg, druhé byly 3 kg a měla o 14 % sušiny více (o 14 procentních bodů více) než první. Třetí směsi, která měla 2 krát tolik % sušiny jako první směs, bylo 6 kg. Kolik % suši - Vinař
Do jaké výšky může vinař naplnit sud rozmačkanými červenými hrozny, jestliže tyto kvašeniny zaujimají objem o 20 procentech? Sud je tvaru válce o průměru podstavy 1 m a objemu 9,42 hl. Vycházej z úvahy, která řiká, že kvašením je zaplněna celá nádoba (čis - Kolikrát 7
Kolikrát se zmenší povrch koule, pokud její poloměr zmenšíme dvakrát? - Zahrada
Otec zryje zahradu za 7 hodin. Syn za 10 hodin. Za kolik hodin zryjú zahradu společně? - Čtyřúhelníku 81469
Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji - Danka a janka
Dvojčata Danka a Janka šli s kamarádkou Betkou do kina. V kině bylo volných už jen 6 sedadel ve druhé řadě. Kolik mají možností usazení, když dvojčata chtějí sedět vedle sebe, Danka vždy vpravo od Janky a Betka při jedné z nich? - Jednociferné číslo
Rozhodněte, zda lze k číslu s ciferným součtem 2024 připočítat jednociferné číslo tak, aby výsledné číslo mělo ciferný součet 74. - Zabarvené 64114
Dřevěnou kostku s hranou délky 4 cm jsme natřeli po celém povrchu zelenou barvou. Potom jsme ji rozřízli na malé kostičky s hranou délky 1 cm. Počet kostek, které mají právě dvě stěny zabarvené zeleně je: - V lichoběžníku 3
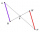V lichoběžníku ABCD jsou dány délky základen |AB| = 12 cm, |CD| = 8 cm. Bod S je průsečík úhlopříček, pro který platí |AS| = 6 cm. Vypočítej délku celé úhlopříčky AC. - JUDr. Lichva
Soudce JUDr. Lichva schválil dohodu o vině a trestu kde přiznal povinnost zaplatit denní úrok 0,23%. O jak velký se jedná o roční úrok? Rok uvažujte jako 365 dnů. - V ovocném
V ovocném sadě vysadili 25 stromků jabloni, 20 hrušek, 15 švestek a 40 meruněk. Silný pozdní mráz však zničil pětinu ze všech nově vysazených stromků. Naneštěstí to byly všechno stromky jednoho druhu ovoce. Jaká je pravděpodobnost, že vymřeli švestky? - Vytvořených 4533
Na tabuli je napsáno pět navzájem různých kladných čísel. Určete největší možný počet dvojic z nich vytvořených, ve kterých je součet obou prvků roven jednomu z pěti čísel napsaných na tabuli. - Potřebuji 44081
Střecha v podobě jehlanu, na domě s půdorysem čtverce má rozměry 12 x 12 m, v nejvyšším bodě výšku 2m. Kolik krytiny potřebuji zakoupit? Počítej s rezervou 10%. - Okapové 3 Okapové žleby mají tvar poloviny válce. Jejich průměr je 20cm, celková délka kolem střechy je 35m. Kolik plechu je potřeba na jejich zhotovení? Připočítej 15% na spoje.
- Rotační pohyb
Jakou minimální rychlostí a frekvencí musíme otáčet ve svislé rovině po kružnici o poloměru 70 cm konví s vodou, aby se voda nevylila? - Zobrazující 33123
Rok; peníze vynaložené na reklamu; zisk (tři hodnoty v každém řádku) 2008 2 12 2009 5 20 25. 7. 2010 2011 11 26 2012 15 40 1. nakreslete rozptylový diagram zobrazující údaje. 2. vypočítejte Pearsonův korelační koeficient. 3. určete rovnici lineární regres - Kolik 139
Kolik cihel je potřeba na stavbu zdi, která má délku 12 m, výšku 1,6 m a šířku 47 cm, je-li rozměr cihly 30 x 15 x 7,5 cm a 5 % objemu zdi tvoří malta? - Objem kvádru
O kolik procent se zvětší objem kvádru, pokud jeho každý rozměr zvětší o 30%? - Bankomatové 28341
Maminka zapomněla PIN kód své bankomatové karty, který tvořily 4 různá čísla. Pomoz jí ho sestavit, pokud si pamatuje, že : A - všechna čísla byla sudá B - nula v pin kode nebyla C - první číslo bylo násobkem druhého čísla a toto číslo bylo v PIN kódu nej
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
