Základní operace a pojmy - slovní úlohy a příklady - strana 278 z 303
Počet nalezených příkladů: 6060
- Napište 3
 Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0.
Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0. - Podobnosť trojuholníkov
 a= 6cm, b=8cm, c=? , a'=? , b'=12cm, c'=15cm
a= 6cm, b=8cm, c=? , a'=? , b'=12cm, c'=15cm - Lichoběžník MO-5-Z8
 Lichoběžník ABCD je úsečkou CE rozdělen na trojúhelník a rovnoběžník, viz obrázek. Bod F je středem úsečky CE, přímka DF prochází středem úsečky BE a obsah trojúhelníku CDE je 3 cm². Určete obsah lichoběžníku ABCD.
Lichoběžník ABCD je úsečkou CE rozdělen na trojúhelník a rovnoběžník, viz obrázek. Bod F je středem úsečky CE, přímka DF prochází středem úsečky BE a obsah trojúhelníku CDE je 3 cm². Určete obsah lichoběžníku ABCD. - Určete 39
 Určete pravděpodobnost, že při třech hodech kostkou padne aspoň jednou 1.
Určete pravděpodobnost, že při třech hodech kostkou padne aspoň jednou 1. - Železnice
 Železnice má stoupání 1,1 ‰. Jaký je výškový rozdíl dvou míst na trati vzdálených navzájem 2269 metrů?
Železnice má stoupání 1,1 ‰. Jaký je výškový rozdíl dvou míst na trati vzdálených navzájem 2269 metrů? - Čas malování školy druhým malířem
 Jeden malíř by vymaloval školu za 15 dní. Společně s druhým malířem vymalovali školu za 6 dní. Za kolik dní by vymaloval školu druhý malíř sám.
Jeden malíř by vymaloval školu za 15 dní. Společně s druhým malířem vymalovali školu za 6 dní. Za kolik dní by vymaloval školu druhý malíř sám. - Podobnost čtverců
 Poměr podobnosti čtverců ABCD a KLMN je 2,5. Obsah čtverce KLMN je větší než obsah čtverce ABCD se stranou a: ...
Poměr podobnosti čtverců ABCD a KLMN je 2,5. Obsah čtverce KLMN je větší než obsah čtverce ABCD se stranou a: ... - Rychlost cyklisty
 Pozorovateľ sedí v miestnosti 2 m od okna širokého 50 cm. Rovnobežne vo vzdialenosti 500 m vedie cesta. Akou veľkou priemernou rýchlosťou ide cyklista po tejto ceste, keď ho pozorovateľ vidí 15 s?
Pozorovateľ sedí v miestnosti 2 m od okna širokého 50 cm. Rovnobežne vo vzdialenosti 500 m vedie cesta. Akou veľkou priemernou rýchlosťou ide cyklista po tejto ceste, keď ho pozorovateľ vidí 15 s? - Podobné trojúhelníky
 Pravoúhlý trojúhelník XYZ je podobný trojúhelníku ABC, který má pravý úhel u vrcholu X. Platí: a = 9 cm, x=4 cm, x =v-4 (v = výška trojúhelníku ABC). Vypočítej chybějící délky stran obou trojúhelníků.
Pravoúhlý trojúhelník XYZ je podobný trojúhelníku ABC, který má pravý úhel u vrcholu X. Platí: a = 9 cm, x=4 cm, x =v-4 (v = výška trojúhelníku ABC). Vypočítej chybějící délky stran obou trojúhelníků. - Denní průměr
 Vypočtěte průměrnou teplotu během dne, pokud 13 hodin bylo 22 °C a 11 hodin bylo 16 °C.
Vypočtěte průměrnou teplotu během dne, pokud 13 hodin bylo 22 °C a 11 hodin bylo 16 °C. - Na univerzitě
 Na určité univerzitě je 25% studentů obchodní fakulty. Ze studentů obchodní fakulty je 66% mužů. Avšak pouze 52% všech studentů na univerzitě jsou muži. a. Jaká je pravděpodobnost, že náhodně vybraný student na univerzitě je muž na obchodní fakultě? b. Ja
Na určité univerzitě je 25% studentů obchodní fakulty. Ze studentů obchodní fakulty je 66% mužů. Avšak pouze 52% všech studentů na univerzitě jsou muži. a. Jaká je pravděpodobnost, že náhodně vybraný student na univerzitě je muž na obchodní fakultě? b. Ja - Výběr 4
 Výběr trojúhelník, který je podobný zadanému trojúhelníku RTG. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. ∆ SHV= 6 dm, h= 7,5 dm, v= 7 dm ∆ VSH= v= 7 dm, s= 6 dm, h= 7,5 dm ∆ HVS= h= 7,5 dm, v= 7 dm, s = 6 dm. ∆ VHS= v= 7 dm, h = 7,5 dm, s= 6 dm. ∆ HSV= h= 7,5
Výběr trojúhelník, který je podobný zadanému trojúhelníku RTG. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. ∆ SHV= 6 dm, h= 7,5 dm, v= 7 dm ∆ VSH= v= 7 dm, s= 6 dm, h= 7,5 dm ∆ HVS= h= 7,5 dm, v= 7 dm, s = 6 dm. ∆ VHS= v= 7 dm, h = 7,5 dm, s= 6 dm. ∆ HSV= h= 7,5 - Vypočítejte 5
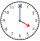 Vypočítejte velikost úhlu, které svírají přímky p a q, které spojují na ciferníku hodin 1, 6(přímka p) a 5, 8(přímka q)
Vypočítejte velikost úhlu, které svírají přímky p a q, které spojují na ciferníku hodin 1, 6(přímka p) a 5, 8(přímka q) - Rozlišení displeje
 Displej má rozlišení 1680 x 1050 pixelů. Jaké jsou souřadnice (a velikost v pixelech) vycentrované oblasti, která je přesně 33 % velikosti obrazovky?
Displej má rozlišení 1680 x 1050 pixelů. Jaké jsou souřadnice (a velikost v pixelech) vycentrované oblasti, která je přesně 33 % velikosti obrazovky? - Šestiúhelník
 Je dán pravidelný šestiúhelník ABCDEF. Je-li obsah trojúhelníku ABC roven 16, pak obsah šestiúhelníku ABCDEF je roven? Nevím, jak na to jednoduše přijít....
Je dán pravidelný šestiúhelník ABCDEF. Je-li obsah trojúhelníku ABC roven 16, pak obsah šestiúhelníku ABCDEF je roven? Nevím, jak na to jednoduše přijít.... - Úhlopříčka TV
 Úhlopříčka TV je dlouhá 0,56 m, jak velký je televizor, při poměru stran 16:9?
Úhlopříčka TV je dlouhá 0,56 m, jak velký je televizor, při poměru stran 16:9? - Obchod
 Ze statistiky prodejnosti zboží se zjistilo, že zboží A si koupí 64% lidí a zboží B si koupí 69% lidí Jaká je pravděpodobnost, že z 5 lidí si 2 koupí A a 3 značku B?
Ze statistiky prodejnosti zboží se zjistilo, že zboží A si koupí 64% lidí a zboží B si koupí 69% lidí Jaká je pravděpodobnost, že z 5 lidí si 2 koupí A a 3 značku B? - Pokladny
 V Tescu je otevřených 10 pokladen. Zákazníci čekají průměrně 15 minut. Kolik dalších pokladen musí ještě otevřít, aby se doba čekání zkrátila o 4 minuty?
V Tescu je otevřených 10 pokladen. Zákazníci čekají průměrně 15 minut. Kolik dalších pokladen musí ještě otevřít, aby se doba čekání zkrátila o 4 minuty? - Rozdělení zlatých kostek
 Král se neumí rozhodnout, jak má co nejspravedlivější rozdělit dvěma synům 4 kostky čistého zlata, které mají hranu délky 3cm, 4cm, 5cm, 6cm. Navrhněte řešení tak, aby se nemusely kostky řezat.
Král se neumí rozhodnout, jak má co nejspravedlivější rozdělit dvěma synům 4 kostky čistého zlata, které mají hranu délky 3cm, 4cm, 5cm, 6cm. Navrhněte řešení tak, aby se nemusely kostky řezat. - Společně
 Dano by posekat trávník za 12 hodin, Milada za 16 hodin. Za jaký čas by posekali trávník společně?
Dano by posekat trávník za 12 hodin, Milada za 16 hodin. Za jaký čas by posekali trávník společně?
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
