Základní operace a pojmy - slovní úlohy a příklady - strana 279 z 303
Počet nalezených příkladů: 6060
- Polohový vektor hmotného bodu
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t = 2s - Měřítko mapy
Jaká je měřítko mapy, pokud úsečka dlouhá 2,5 cm představuje 500 km? - Nadměrná rezervace
Malý regionální dopravce přijal 12 rezervací na konkrétní let s 11 sedadly. Sedm rezervací šlo běžným zákazníkům, kteří na let dorazí. Každý zbývající cestující dorazí na let se 49% šancí, nezávisle na sobě. (Odpovědi uveďte s přesností na 4 desetinná mís - Jedna správná v testu
V testu je šest otázek. Ke každé jsou nabídnuty 3 odpovědi - z nich je pouze jedna správná. K tomu, aby student udělal zkoušku, třeba správně odpovědět alespoň na čtyři otázky. Alan se vůbec neučil, a tak odpovědi zakrúžkovával pouze hádáním. Jaká je prav - Kolik 21
Kolik gramů pevného CuSO4 musíme přidat do 450g 15% roztoku CuSO4, aby vznikl 25% roztok? - Číslice trojciferných čísel
Vírka ze tří daných číslic sestavovala navzájem různá trojmístné čísla. Když všechna tato čísla sečetla, vyšlo jí 1554. Jaké číslice Vierka použila? - Malování bytu
Otec se synem společně vymalují byt za 6 hodin. Otec by sám vymaloval byt za 9 hodin. Za kolik hodin by byt vymaloval syn sám? - Uhodne celej test
Test obsahuje 4 otázky a na každou z nich je 5 různých odpovědí, z nichž je správná jen jedna, ostatní jsou nesprávné. Jaká je pravděpodobnost, že žák, který nezná odpověď na žádnou otázku, uhodne správné odpovědi na všechny otázky? - Polohový vektor
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době - Ocet 2
Kolika procentní roztok dostaneme, smícháme-li 3,5 litru 5,9% octa a 4,5 litru 7,8% octa? - 9 obdélníků
Velký obdélník je rozdělen na 9 malých obdélníků. Kolik je tam spolu obdélníků? - Pravděpodobnost - hřídele
Předpokládejme, že 14 % všech ocelových hřídelů vyrobených určitým procesem je neshodných, ale lze je přepracovat (a ne sešrotovat). Vezměme si náhodný vzorek 200 hřídelí a nechť X označuje počet z nich, které nejsou v souladu a mohou být přepracovány. a) - Polohový vektor Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době
- Rovnice elipsy body A, B
Napište rovnici elipsy, která prochází body a její osy jsou totožné se souřadnicovými osami, když: A = [2, 3] a B = [−1, −4]. - Kontrola zmetků Ze série výrobků se má zkontrolovat 500 kusů, přičemž se provádí kontrola s opakováním. Výrobce garantuje při dané výrobě 2% zmetků. Určete pravděpodobnost, že mezi 500 kontrolovanými výrobky bude počet zmetků od 12 do 20.
- Pravděpodobnost nápojů
V zemi pije kávu 65 % lidí, 50 % pije čaj a 25 % pije obojí. Jaká je pravděpodobnost, že náhodně vybraná osoba nebude pít ani čaj ani kávu? - Násobení tří členů
Kolik různých množin kladného celého čísla ve tvaru (x, y, z) ke splnění rovnice xyz=1400? - Pravděpodobnost - test
Test obsahuje 11 otázek, přičemž každá otázka má 4 možnosti (pouze jedna správná). Zjistěte pravděpodobnost, že na méně než 2 otázky/otázek odpoví správně. (Pravděpodobnost správně zodpovězené otázky je 1/4.) (Výsledek zapište jako celé číslo v procentech - Nejmenší součet vzdáleností
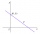Je dána přímka p a dva vnitřní body jedné z polorovin, určených přímkou p. Najdi na přímce p bod X tak, aby součet jeho vzdáleností od bodů A, B byl nejmenší. - Propuštění zaměstnanců
V jednom úřadě pracuje 7 žen a 3 muži. Podle nového nařízení je nutné snížit počet zaměstnanců o třech. Jaká je pravděpodobnost, že při náhodném výběru zaměstnanců budou propuštěni: a. Jedna žena a dva muži b. Alespoň jedna žena
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
