Planimetrics - math word problems - page 160 of 185
Number of problems found: 3685
- Square 81238
 A forest with a square plan has an area of 4 square km. What side will the square have on a 1:50,000 scale map?
A forest with a square plan has an area of 4 square km. What side will the square have on a 1:50,000 scale map? - Elevation of the tower
 We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower
We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower - Depth angle
 Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115 m above the lake level.
Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115 m above the lake level. - The sequence
 Find the nth term of the progression 2,6,12,20...
Find the nth term of the progression 2,6,12,20... - Track arc
 Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)?
Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)? - The chimney
 How high is the chimney if we see it from a distance of 60 m at an angle of 42°?
How high is the chimney if we see it from a distance of 60 m at an angle of 42°? - Tourist 39691
 How far from the lookout tower, 48 m high, did the tourist stand if he saw its top at an angle of 40°?
How far from the lookout tower, 48 m high, did the tourist stand if he saw its top at an angle of 40°? - Two cables
 On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag.
On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag. - Right triangle
 It is given a right triangle angle alpha of 90 degrees the beta angle of 55 degrees c = 10 cm use the Pythagorean theorem to calculate sides a and b
It is given a right triangle angle alpha of 90 degrees the beta angle of 55 degrees c = 10 cm use the Pythagorean theorem to calculate sides a and b - Shooter
 The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot?
The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot? - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Determine 8202
 An observer watches two boats at depth angles of 64° and 48° from the top of the hill, which is 75 m above the lake level. Determine the distance between the boats if both boats and the observer are in the same vertical plane.
An observer watches two boats at depth angles of 64° and 48° from the top of the hill, which is 75 m above the lake level. Determine the distance between the boats if both boats and the observer are in the same vertical plane. - Altitude angles
 Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi
Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi - Triangle α and side
 Side a in the right triangle has size a = 120 mm, angle α = 60°. How big is the hypotenuse c?
Side a in the right triangle has size a = 120 mm, angle α = 60°. How big is the hypotenuse c? - Percentage 80164
 I was given a square ABCD 4.2 cm. Find the set of all points that have a distance less than or equal to 2 cm from one of its vertices and lie inside this square. Indicate how much of the square this area occupies as a percentage.
I was given a square ABCD 4.2 cm. Find the set of all points that have a distance less than or equal to 2 cm from one of its vertices and lie inside this square. Indicate how much of the square this area occupies as a percentage. - Embankment 7879
 An embankment 7.5 m high should be built on the horizontal plane. The width of the upper surface of the embankment is 2.9 m, and the slope is 35 °. What will be the lower width of the embankment?
An embankment 7.5 m high should be built on the horizontal plane. The width of the upper surface of the embankment is 2.9 m, and the slope is 35 °. What will be the lower width of the embankment? - Trapezoid MO-5-Z8
 ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi
ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi - Altitude angle
 In complete winds-free weather, the balloon took off and remained standing exactly above the place from which it took off. It is 250 meters away from us. How high did the balloon fly when we saw it at an altitude angle of 25°?
In complete winds-free weather, the balloon took off and remained standing exactly above the place from which it took off. It is 250 meters away from us. How high did the balloon fly when we saw it at an altitude angle of 25°? - A ship
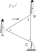 A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57°
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Inner angles
 The inner angles of the triangle are 30°, 45°, and 105° and its longest side is 10 cm. Calculate the shortest side length, and write the result in cm up to two decimal places.
The inner angles of the triangle are 30°, 45°, and 105° and its longest side is 10 cm. Calculate the shortest side length, and write the result in cm up to two decimal places.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
