Postupnosť
Vypočítajte, koľký člen postupnosti určenej vzťahom {3n−1+50} má hodnotu 59.
Správna odpoveď:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebrazákladné operácie a pojmyÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Tretí člen
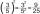Určte, akú hodnotu bude mať tretí člen postupnosti, ak je postupnosť daná vzťahom: 3^n+93. - Určenie postupnosti
Je daná postupnosť, ktorej prvými tromi členmi sú a1= 70, a2=64, a3=58. 1, rozhodnete, či sa jedna o aritmetickú alebo geometrickú postupnosť a podľa toho určite hodnotu d respektíve q. 2, určite hodnotu pätnásteho členov postupnosti. 3, určite, koľký čle - AP - d a a1
Vypočítajte hodnotu prvého člena a diferenciu aritmetickej postupnosti a1+a7=42 a10-a3=21 - GP tri členy
Druhý a tretí člen geometrickej postupnosti sú 24 a 12(c+1) v tomto poradí. Za predpokladu, že súčet prvých troch členov postupnosti je 76, určite hodnotu c. - AP 6
Vypočítajte prvých 5 členov aritmetickej postupnosti, ak je dané: a2 – a3 + a5 = 20 a1 + a6 = 38 - Postupnosť
Zapíšte prvých 5 členov tejto postupnosti: a1 = -7 a2 = 6 an+2 = an+1 -1 an - Funkcia
Napíšte prvých päť členov postupnosti a_n =(3n - (-1)^n) +2
