Na ihrisku 2
Na ihrisku sú nakreslené tri rovnako veľké kruhy. Rozostavte 16 kolkov tak, aby v každom kruhu stálo 9 kolkov. Nájdite aspoň osem podstatne odlišných rozostavení, t. J. takých rozostavení, pri ktorých sa nerozlišujú kolky ani kruhy.
Správna odpoveď:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebrazákladné operácie a pojmyčíslaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- V krabici 2
V krabici je 11 výrobkov, z ktorých sú práve 4 chybné. Koľkými spôsobmi môžeme vybrať 5 výrobkov tak, aby aspoň štyri neboli chybné? - Vežu z kociek
Koľkými spôsobmi je možné zostaviť vežu z piatich žltých a štyroch modrých kociek tak, aby každá žltá kocka susedila s aspoň jednou ďalšou žltou kockou? Žlté kocky sú nerozlíšiteľné a rovnako tak modré kocky. - Záhony
Pred športovou halou sú dva rovnako veľké obdĺžnikové záhony trávniku, každý s rozmermi 40 m a 12 m. Údržba 10 m² trávnika stojí ročne 45 Kč (českých korún). Na každom záhone je kruhový kvetinový záhon o priemere 8 m. S koľkými korunami treba ročne počíta - Snehuliak
V kruhu o priemere 44 cm sú narysované 3 kruhy / ako snehuliak / pre ktoré platí: priemery sú celočíselné, priemer každého väčšieho kruhu je o 2 cm väčší ako priemer predchádzajúceho kruhu. Urči výšku snehuliaka, tak aby bol najvyšší. - Strecha
Na streche tvaru lichobežníka sú poukladané škridly do radov tak, že pri hrebeni je 35 škridiel a v každom nasledujúcom rade je o jednu škridlu viac než v predchádzajúcom rade. Koľkými škridlami je pokrytá strecha, ak najspodnejší rad má 71 škridiel? - Lichobežník ABCD
Obrázok ukazuje, že ABDC je lichobežník, v ktorom AB || CD. Úsečky RN a LM sú nakreslené rovnobežne s AB tak, že AJ=JK=KP. Ak AB=0,5 m a AP=BQ=1,8 m, nájdite dĺžky AC, BD, RN a LM. uhol D=uhol C=60 - Menší kruh
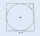Dva kruhy sú vpísané do štvorca, ktorého strana je 4 cm. Nájdite polomer menšieho kruhu.
