Fibonacciho čísla
Ak sú prvé tri Fibonacciho čísla dané ako x1 = 1, x2 = 1 a x3 = 2, aká je najmenšia hodnota n, pre ktorú x(n) > 500?
Správna odpoveď:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikačíslaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Najmenšia hodnota
Aká najmenšia hodnota musí byť priradená písmenku x, aby číslo 789x563 bolo deliteľné 3? - Tri body
Sú dané tri body v rovine A (-3; -5) B (9; -10) a C (2; k). Dĺžka AB = AC Aká je hodnota k? - Otvorené intervaly
Dané sú otvorené intervaly A=(x-2; 2x-1) a B=(3x-4; 4). Nájdite najväčšie reálne číslo, pre ktoré platí A ⊂ B. - Prvý test
Pre test je pripravených 20 otázok. Z nich sú pre prvý test vybrané 3 otázky. Tie sú do zoznamu vrátené. Aká je pravdepodobnosť, že pri výbere pre druhý test budú vybrané rovnaké 3 otázky ako pre prvé? - Sú dané
Sú dané vektory a = (4,2), b = (- 2,1). Vypočítajte: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|. - Skalárne súčiny
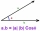Dané sú vektory a = (3, -2), b = (-1, 5). Určte vektor c, pre ktorý platí a. c = 17, b. c = 3 - Delitele
Sú dané dve čísla. Druhé číslo je päťkrát väčšie ako prvé číslo a druhá mocnina prvého čísla sa rovná 3/5 druhého čísla, určite súčet oboch čísel a všetkých jeho deliteľov.
