Príklady pre stredoškolákov - strana 45 z 225
Počet nájdených príkladov: 4484
- Semenáčiky
 Paseka bola rozdelená na 30 rovnako veľkých častí a následne bolo spočítané, koľko semenáčikov sa nachádza v jednotlivých častiach. Zistilo sa, že v šiestich častiach sa nenachádzal žiadny semenáčik, päť častí obsahovalo jeden semenáčik, dvanásť častí dva
Paseka bola rozdelená na 30 rovnako veľkých častí a následne bolo spočítané, koľko semenáčikov sa nachádza v jednotlivých častiach. Zistilo sa, že v šiestich častiach sa nenachádzal žiadny semenáčik, päť častí obsahovalo jeden semenáčik, dvanásť častí dva - Chí kvadrát 2
 Nech za posledných 14 rokov mala krajina tieto miery inflácie: 6,0; 6,7; 10,4; 11,9; 7,2;3,5; 8,4; 7,5; 2,8; 4,3; 1,9; 3,9; 0,9; 0,7. Pomocou χ² testu dobrej zhody zistite, či náhodná veličina ξ odpovedajúca tejto miere inflácie má normálne rozdelenie ale
Nech za posledných 14 rokov mala krajina tieto miery inflácie: 6,0; 6,7; 10,4; 11,9; 7,2;3,5; 8,4; 7,5; 2,8; 4,3; 1,9; 3,9; 0,9; 0,7. Pomocou χ² testu dobrej zhody zistite, či náhodná veličina ξ odpovedajúca tejto miere inflácie má normálne rozdelenie ale - Povrch 24
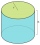 Povrch valca je 1570 cm², jeho výška je 15 cm. Určte jeho objem a polomer podstavy.
Povrch valca je 1570 cm², jeho výška je 15 cm. Určte jeho objem a polomer podstavy. - Pri vyberaní
 Pri vyberaní kameňa z vody sme pôsobili silou 120N. Akou veľkou silou budeme musieť pôsobiť, ak budeme kameň premiestňovať nad vodnou hladinou? Hustota kameňa je 5000 kg/m³.
Pri vyberaní kameňa z vody sme pôsobili silou 120N. Akou veľkou silou budeme musieť pôsobiť, ak budeme kameň premiestňovať nad vodnou hladinou? Hustota kameňa je 5000 kg/m³. - Jeden
 Jeden robotník zhotoví určitú súčiastku o 4 hodiny a druhý robotník o 9 hodín neskôr, než by zhotovili rovnakú súčiastku spoločne. Za akú dobu zhotoví súčiastku každý robotník sám?
Jeden robotník zhotoví určitú súčiastku o 4 hodiny a druhý robotník o 9 hodín neskôr, než by zhotovili rovnakú súčiastku spoločne. Za akú dobu zhotoví súčiastku každý robotník sám? - Vzduch termika
 Vo valci s objemom V0 je uzavretý vzduch. Teplota vzduchu je T a tlak je p0. Pri udržaní konštantnej teploty je najprv vzduch piestom stlačený na šestinu objemu. Následne po veľmi rýchlom otvorení a zatvorení ventilu na valci dôjde k expanzii vzduchu na d
Vo valci s objemom V0 je uzavretý vzduch. Teplota vzduchu je T a tlak je p0. Pri udržaní konštantnej teploty je najprv vzduch piestom stlačený na šestinu objemu. Následne po veľmi rýchlom otvorení a zatvorení ventilu na valci dôjde k expanzii vzduchu na d - Na majstrovstvách
 Na majstrovstvách sveta 2021 v hokeji je v skupine A 8 mužstiev, každé z nich hrá 7 zápasov, v každom zápase sú pre každé mužstvo 4 možnosti získania bodov (3-2-1-0), vždy je to ale spárované s bodmi súpera (0-1-2-3). Koľko existuje možností rozdelenia bo
Na majstrovstvách sveta 2021 v hokeji je v skupine A 8 mužstiev, každé z nich hrá 7 zápasov, v každom zápase sú pre každé mužstvo 4 možnosti získania bodov (3-2-1-0), vždy je to ale spárované s bodmi súpera (0-1-2-3). Koľko existuje možností rozdelenia bo - Postavenie veží
 Koľkými spôsobmi môžeme na šachovnici 8×8 postaviť 8 nerozlíšiteľných veží tak, aby sa neohrozovali?
Koľkými spôsobmi môžeme na šachovnici 8×8 postaviť 8 nerozlíšiteľných veží tak, aby sa neohrozovali? - Dve autá
 Dve autá (nákladné a osobné) vycestovala súčasne z dvoch miest vzdialených 50 km. Idú Ak proti sebe, stretnú sa za 30 minút. Idú Ak rovnakým smerom za sebou, dobehne osobné auto nákladné za 2,5 hodiny. Aká je rýchlosť každého z nich?
Dve autá (nákladné a osobné) vycestovala súčasne z dvoch miest vzdialených 50 km. Idú Ak proti sebe, stretnú sa za 30 minút. Idú Ak rovnakým smerom za sebou, dobehne osobné auto nákladné za 2,5 hodiny. Aká je rýchlosť každého z nich? - Harmonické kmitanie
 Napíšte rovnicu harmonického kmitania, ak je amplitúda kmitania 5 cm a jeho perióda 0,5 s.
Napíšte rovnicu harmonického kmitania, ak je amplitúda kmitania 5 cm a jeho perióda 0,5 s. - Fľaša 3
 Fľaša a pohár majú rovnakú hmotnosť ako krčah. Fľaša má takú istú hmotnosť ako pohár a tanier. Dva krčahy majú rovnakú hmotnosť ako tri tanier. Akú hmotnosť má fľaša, ak hmotnosť pohára je 100g.
Fľaša a pohár majú rovnakú hmotnosť ako krčah. Fľaša má takú istú hmotnosť ako pohár a tanier. Dva krčahy majú rovnakú hmotnosť ako tri tanier. Akú hmotnosť má fľaša, ak hmotnosť pohára je 100g. - Úspory súrodencov
 Traja súrodenci mali ušetrených 1445 Kč. Adela mala ušetrených o 10% menej ako Martin, David o 10% viac ako Adela. Koľko korún mal ušetrených každý z nich?
Traja súrodenci mali ušetrených 1445 Kč. Adela mala ušetrených o 10% menej ako Martin, David o 10% viac ako Adela. Koľko korún mal ušetrených každý z nich? - Výška stožiaru
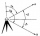 Traja geodeti majú za úlohu zmerať výšku stožiara stojaceho na rovnej pláni. Prvý merač stojaci 100 m od stožiara zmeral výškový uhol (a), druhý vzdialený 200 m od stožiara zmeral výškový uhol (b) a tretí zo vzdialenosti 300 m od stožiara zmeral výškový u
Traja geodeti majú za úlohu zmerať výšku stožiara stojaceho na rovnej pláni. Prvý merač stojaci 100 m od stožiara zmeral výškový uhol (a), druhý vzdialený 200 m od stožiara zmeral výškový uhol (b) a tretí zo vzdialenosti 300 m od stožiara zmeral výškový u - Časový signál
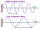 Časový signál v rozhlase je tvorený štyrmi zvukovými značkami s frekvenciou 1 000 Hz, z ktorých prvé tri majú trvanie po 100 ms a štvrtá 500 ms. Koľko kmitov pri každej značke prebehne?
Časový signál v rozhlase je tvorený štyrmi zvukovými značkami s frekvenciou 1 000 Hz, z ktorých prvé tri majú trvanie po 100 ms a štvrtá 500 ms. Koľko kmitov pri každej značke prebehne? - Frekvencie
 Za 24 s vykonalo prvý kyvadlo 12 kmitov a druhé 16 kmitov. Určte periódy a frekvencie oboch kyvadiel.
Za 24 s vykonalo prvý kyvadlo 12 kmitov a druhé 16 kmitov. Určte periódy a frekvencie oboch kyvadiel. - Teleso na nosníku
 Na nosníku s hmotnosťou 100 kg a dĺžkou 5 m je zavesené vo vzdialenosti 1 m od jedného konca nosníka teleso s hmotnosťou 400 kg. Aké veľké sily pôsobia na koncoch nosníka?
Na nosníku s hmotnosťou 100 kg a dĺžkou 5 m je zavesené vo vzdialenosti 1 m od jedného konca nosníka teleso s hmotnosťou 400 kg. Aké veľké sily pôsobia na koncoch nosníka? - RR lichobežník
 Vypočítajte výšku v rovnoramennom lichobežníka, ak je obsah 520 cm² a základne a = 25 cm a c = 14cm. Vypočítajte vnútorné uhly lichobežníka.
Vypočítajte výšku v rovnoramennom lichobežníka, ak je obsah 520 cm² a základne a = 25 cm a c = 14cm. Vypočítajte vnútorné uhly lichobežníka. - Coulombov zákon
 Tri rovnaké kladné náboje Q sú umiestnené vo vrcholoch rovnoramenného pravouhlého trojuholníka ABC. Pravý uhol je pri vrchole A. Dĺžka strany AB je 1 m. Aká je intenzita elektrického poľa v strede S strany BC, t. j. aká sila by pôsobila na kladný náboj q
Tri rovnaké kladné náboje Q sú umiestnené vo vrcholoch rovnoramenného pravouhlého trojuholníka ABC. Pravý uhol je pri vrchole A. Dĺžka strany AB je 1 m. Aká je intenzita elektrického poľa v strede S strany BC, t. j. aká sila by pôsobila na kladný náboj q - Chi kvadrát
 Porovnával sa počet zamestnancov v oblasti kultúry v krajine A a v krajine B. Zistili sa tieto počty zamestnancov v tis. Osôb: krajina A x/46/45/41/48/49/ krajina B y/128/135/147/152/148/. Na hladine testu α=0,05 zistite, či počet zamestnancov v oblasti k
Porovnával sa počet zamestnancov v oblasti kultúry v krajine A a v krajine B. Zistili sa tieto počty zamestnancov v tis. Osôb: krajina A x/46/45/41/48/49/ krajina B y/128/135/147/152/148/. Na hladine testu α=0,05 zistite, či počet zamestnancov v oblasti k - Bezpečnostné normy
 Stroj vyrába oceľové tyče s normálne rozloženou dĺžkou, pričom stredná dĺžka je 50,0 cm a štandardná odchýlka je 0,5 cm. Prúty nespĺňajú bezpečnostné normy, ak sú kratšie ako 49,1 cm alebo dlhšie ako 50,7 cm. Nájdite počet prútov zo zásielky 5000 prútov,
Stroj vyrába oceľové tyče s normálne rozloženou dĺžkou, pričom stredná dĺžka je 50,0 cm a štandardná odchýlka je 0,5 cm. Prúty nespĺňajú bezpečnostné normy, ak sú kratšie ako 49,1 cm alebo dlhšie ako 50,7 cm. Nájdite počet prútov zo zásielky 5000 prútov,
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
