Príklady na trojuholník - strana 25 z 125
Počet nájdených príkladov: 2482
- Túra po hore
 Turista plánuje túru na jednu stranu hory a nadol na druhej strane vrcholu hory, pričom každá strana hory je tvorená priamkou. Uhol elevácie v počiatočnom bode je 42,4 stupňa a uhol elevácie na konci je 48,3 stupňa_ Horizontálna vzdialenosť medzi počiatoč
Turista plánuje túru na jednu stranu hory a nadol na druhej strane vrcholu hory, pričom každá strana hory je tvorená priamkou. Uhol elevácie v počiatočnom bode je 42,4 stupňa a uhol elevácie na konci je 48,3 stupňa_ Horizontálna vzdialenosť medzi počiatoč - MO Z9 2019 domáce kolo
 V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC.
V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC. - Vyjadrite 11
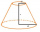 Vyjadrite povrch a objem zrezaného kužeľa pomocou jeho strany s, ak pre polomery podstáv r1 a r2 platí: r1 > r2, r2 = s a ak odchýlka strany od roviny podstavy je 60°.
Vyjadrite povrch a objem zrezaného kužeľa pomocou jeho strany s, ak pre polomery podstáv r1 a r2 platí: r1 > r2, r2 = s a ak odchýlka strany od roviny podstavy je 60°. - Kolmé cesty
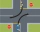 Dve cesty spolu zvierajú pravý uhol. Na jednej ceste je 5km od križovatky namiesto P, na druhej ceste je 12km od križovatky namiesto R. Miesta P a R sú spojené priamou cestičkou. Chodec ide z miesta R do miesta P chodníkom priemernou rýchlosťou 5km/h, aut
Dve cesty spolu zvierajú pravý uhol. Na jednej ceste je 5km od križovatky namiesto P, na druhej ceste je 12km od križovatky namiesto R. Miesta P a R sú spojené priamou cestičkou. Chodec ide z miesta R do miesta P chodníkom priemernou rýchlosťou 5km/h, aut - Teleso, trenie
 Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou?
Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou? - Prúd vody
 Chlapec vesluje na loďke rýchlosťou veľkosti 7,2 km/h . Loďku nasmeroval kolmo na protiľahlý breh vzdialený 600m . Rieka unáša loďku rýchlosťou 4,0 km/h. Aká je výsledná rýchlosť loďky vzhľadom na breh ? Ako ďaleko unesie rieka loďku od miesta, kde by mal
Chlapec vesluje na loďke rýchlosťou veľkosti 7,2 km/h . Loďku nasmeroval kolmo na protiľahlý breh vzdialený 600m . Rieka unáša loďku rýchlosťou 4,0 km/h. Aká je výsledná rýchlosť loďky vzhľadom na breh ? Ako ďaleko unesie rieka loďku od miesta, kde by mal - Tretina kužeľa
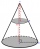 Objem pravého kruhového kužeľa je 5 litrov. Vypočítajte objem dvoch častí, na ktoré je kužeľ rozdelený rovinou rovnobežnou so základňou, v jednej tretine vzdialenosti od vrcholu k základni.
Objem pravého kruhového kužeľa je 5 litrov. Vypočítajte objem dvoch častí, na ktoré je kužeľ rozdelený rovinou rovnobežnou so základňou, v jednej tretine vzdialenosti od vrcholu k základni. - Rýchlosť člna
 Motorový čln sa pohybuje vzhľadom na vodu stálou rýchlosťou 13 m/s. Rýchlosť vodného prúdu v rieke je 5 m/s a) Pod akým uhlom vzhľadom na vodný prúd musí čln plávať, aby sa stále pohyboval kolmo k brehom rieky? b) Akou veľkou rýchlosťou sa približuje čln
Motorový čln sa pohybuje vzhľadom na vodu stálou rýchlosťou 13 m/s. Rýchlosť vodného prúdu v rieke je 5 m/s a) Pod akým uhlom vzhľadom na vodný prúd musí čln plávať, aby sa stále pohyboval kolmo k brehom rieky? b) Akou veľkou rýchlosťou sa približuje čln - Rieka
 Vypočítajte o koľko promile priemerne klesá rieka Hudson, ak na úseku dlhom 766 km tečie voda z výšky 1677 m nad morom na výšku 119 m nad morom.
Vypočítajte o koľko promile priemerne klesá rieka Hudson, ak na úseku dlhom 766 km tečie voda z výšky 1677 m nad morom na výšku 119 m nad morom. - Železnica
 Železničná trať mala na úseku dlhom 5,8 km stúpanie 9 promile. O koľko metrov trať stúpla?
Železničná trať mala na úseku dlhom 5,8 km stúpanie 9 promile. O koľko metrov trať stúpla? - Vypočítaj 349
 Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°.
Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°. - Radar - výškový uhol
 V akej výške letí lietadlo, ktoré zameral radar pod výškovým uhlom 15°24' a priama vzdialenosť lietadla od radaru 5545 m?
V akej výške letí lietadlo, ktoré zameral radar pod výškovým uhlom 15°24' a priama vzdialenosť lietadla od radaru 5545 m? - Parašutista
 Po otvorení padáku klesá výsadkár k zemi stálou rýchlosťou 2 m/s, pričom ho unáša bočný vietor stálou rýchlosťou 1,5 m/s. Určite: a) veľkosť jeho výslednej rýchlosti vzhľadom k zemi, b) vzdialenosť miesta jeho dopadu od osamelého stromu, nad ktorým sa n
Po otvorení padáku klesá výsadkár k zemi stálou rýchlosťou 2 m/s, pričom ho unáša bočný vietor stálou rýchlosťou 1,5 m/s. Určite: a) veľkosť jeho výslednej rýchlosti vzhľadom k zemi, b) vzdialenosť miesta jeho dopadu od osamelého stromu, nad ktorým sa n - Skratka
 Predstavte si, že idete ku kamarátovi po rovnej ceste. Tá cesta má dĺžku 170 metrov. Potom zahnete doprava a pôjdete ďalších 1000 metrov a ste u kamaráta. Otázka znie, o koľko bude kratšia cesta, keď pôjdete priamou cestou cez pole?
Predstavte si, že idete ku kamarátovi po rovnej ceste. Tá cesta má dĺžku 170 metrov. Potom zahnete doprava a pôjdete ďalších 1000 metrov a ste u kamaráta. Otázka znie, o koľko bude kratšia cesta, keď pôjdete priamou cestou cez pole? - Trojboký hranol
 Vypočítaj obsah plášťa pravidelného trojbokého hranola, ak je dĺžka jeho podstavnej hrany 6,5 cm a výška 0,2m.
Vypočítaj obsah plášťa pravidelného trojbokého hranola, ak je dĺžka jeho podstavnej hrany 6,5 cm a výška 0,2m. - Zrezaný 13
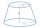 Zrezaný rotačný kužeľ má podstavy s polomermi r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Aký je objem kužeľa, z ktorého zrezaný kužeľ vznikol?
Zrezaný rotačný kužeľ má podstavy s polomermi r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Aký je objem kužeľa, z ktorého zrezaný kužeľ vznikol? - Z9 – I – 2 MO 2018
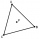 V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM.
V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM. - Dve cesty
 Dve priame cesty sa križujú a zvierajú uhol alfa= 53 stupňov 30'. Na jednej z nich stoja dva stĺpy, jeden na križovatke, druhý vo vzdialenosti 500m od nej. Ako ďaleko treba ist od križovatky po druhej ceste, aby sme videli obidva stĺpy v zornom uhle beta?
Dve priame cesty sa križujú a zvierajú uhol alfa= 53 stupňov 30'. Na jednej z nich stoja dva stĺpy, jeden na križovatke, druhý vo vzdialenosti 500m od nej. Ako ďaleko treba ist od križovatky po druhej ceste, aby sme videli obidva stĺpy v zornom uhle beta? - Úloha o pohybe
 Z križovatky dvoch kolmých ciest vyšli súčasne dvaja cyklisti (každý inou cestou) jeden ide priemernou rýchlosťou 21 km/h, druhý priemernou rýchlosťou 29 km/h. Určte ich vzájomnú vzdialenosť po 40 minútach jazdy.
Z križovatky dvoch kolmých ciest vyšli súčasne dvaja cyklisti (každý inou cestou) jeden ide priemernou rýchlosťou 21 km/h, druhý priemernou rýchlosťou 29 km/h. Určte ich vzájomnú vzdialenosť po 40 minútach jazdy. - Rýchlosť lodníka
 Po palube lodí kráča lodník stálou rýchlosťou 5 km/h v smere, ktorý zviera so smerom rýchlosti lode uhol 60°. Loď sa pohybuje vzhľadom na pokojnú hladinu jazera stálou rýchlosťou 10 km/h. Určite graficky veľkosť rýchlosti, ktorou sa lodník pohybuje vzhľad
Po palube lodí kráča lodník stálou rýchlosťou 5 km/h v smere, ktorý zviera so smerom rýchlosti lode uhol 60°. Loď sa pohybuje vzhľadom na pokojnú hladinu jazera stálou rýchlosťou 10 km/h. Určite graficky veľkosť rýchlosti, ktorou sa lodník pohybuje vzhľad
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
