Vypočítaj 349
Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°.
Vaša odpoveď:
Vaša odpoveď:
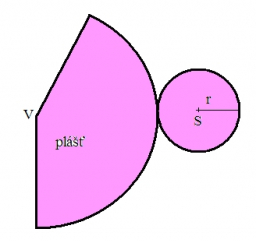
Tipy na súvisiace online kalkulačky
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikastereometriaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Odchýlka podstavy a bočnej strany
Povrch rotačného kužeľa je 30 cm2, obsah jeho plášťa je 20 cm². Vypočítajte odchýlku strany tohto kužeľa od roviny podstavy. - Vypočítaj 70
Vypočítaj povrch a objem rotačného kúžeľa, ak obvod jeho podstavy je 62,8 m a strana má dĺžku 25 m. - Vypočítaj rot kužeľ
Základné parametre rotačného kužeľa sú: Polomer podstavy 5 cm Výška kužeľa 12 cm a strana kužeľa 13 cm. Vypočítaj: a/objem kužeľa b/povrch kužeľa - Strana a obvod kúžeľa
Vypočítaj povrch a objem rotačného kužeľa, ak jeho strana je dlhá 150 mm a obvod podstavy je 43,96 cm. - Vypočítaj - podstava Vypočítajte povrch a objem rotačného kužeľa, ktorého obvod podstavy je 125,6 cm a strana má dĺžku 25 cm.
- Kúžeľ
Objem rotačného kužeľa je 9,42 cm3, pričom výška je rovná 10 cm. Aký uhol zviera strana kužeľa s rovinnou podstavy? - Vyjadrite 11
Vyjadrite povrch a objem zrezaného kužeľa pomocou jeho strany s, ak pre polomery podstáv r1 a r2 platí: r1 > r2, r2 = s a ak odchýlka strany od roviny podstavy je 60°.
